跳转至

Lecture 1: AVL Trees, Splay Trees, and Amortized Analysis

AVL 树、伸展树和摊还分析。

1 AVL Trees

  • Target: Speed up searching(with insertion and deletion). 加快二叉树搜索速度。
  • Tool: Binary Search Trees
  • Problem: The height of the tree can be as bad as \(O(N)\).

一般的二叉搜索树存在问题：树的高度与输入序列有关。例如当我们输入递增/递减序列来构建二叉搜索树的话，树的高度就变成了 \(N\)。而由于动态问题中不能确定下一个输入的值是多少，因此要重新排列输入序列来获得平衡树是不可能的。

因此解决问题的角度变为时刻盯紧这棵树，一有新元素加入就重新拾掇使之平衡。这也是 AVL 树（Adelson-Velskii-Landis Trees, 1962）的思想。

定义：Height Balanced(高度平衡)

An empty binary tree is height balanced. If \(T\) is a nonempty binary tree with \(T_{L}\) and \(T_{R}\) as its left and right subtrees, then \(T\) is height balanced iff:

  1. \(T_{L}\) and \(T_{R}\) are height balanced, and
  2. \(|h_{L}-h_{R}|\leq 1\) where \(h_{L}\) and \(h_{R}\) are the heights of \(T_{L}\) and \(T_{R}\), respectively.

注意

空树的高度定义为 -1。

AVL 树的一种实现方法就是时刻关注 BF 值，对树进行调整使之平衡。

定义：Balance Factor(平衡因数)

\(BF(\mathrm{node})=h_{L}-h_{R}\). In an AVL tree, \(BF(\mathrm{node})=-1, 0, \mathrm{or}\ 1.\)

在加入新的结点的时候，BF 值自下而上更新。

接下来介绍 AVL 树进行调整的几种情况：

1.1 Single Rotation

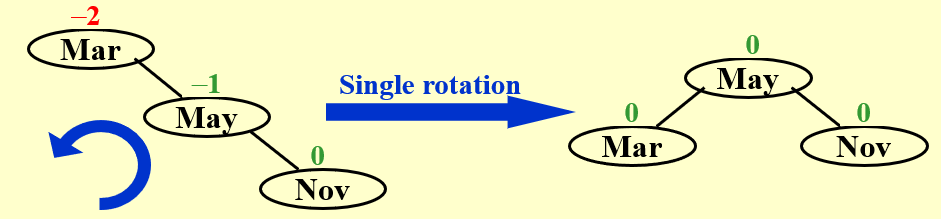
image-20240302131432696

情况如上。

加入 Nov 结点之后，更新 BF 值，发现 Mar 的 BF 值已经不满足 AVL 树的条件了。此时进行单旋（Single Rotation），将 Mar 旋转下来作为 May 的左子树。因为这个问题的 "Trouble Maker" 是 "Trouble Finder" 的右子树的右子树，所以这种操作又称为 RR Rotation。

同理，也有 LL Rotation，不再赘述。

一般化此情况，即为：

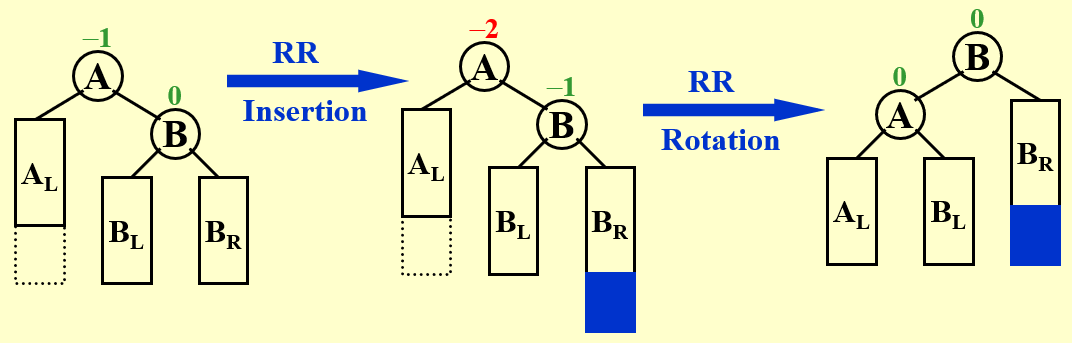
image-20240302132044944

提示

这里的 \(A\) 可以不是树根。

1.2 Double Rotation

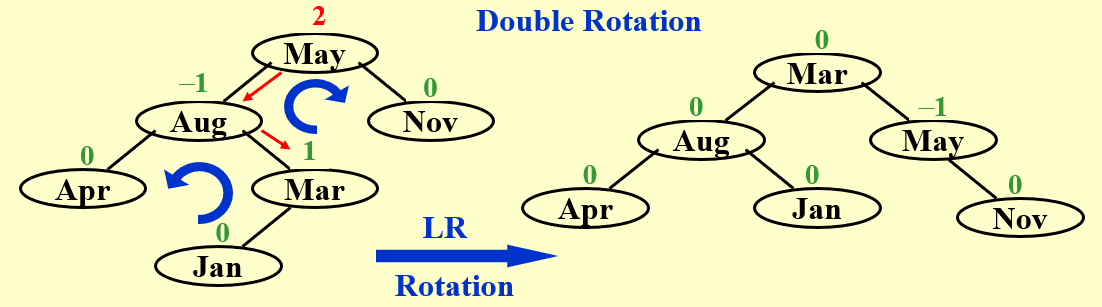
image-20240302133117809

情况如上。

加入 Jan 结点后，May 的 BF 值不满足条件，此时将 Mar 拎上去作为树根，原来的 May 就作为它的右儿子即可。这种情况下的 "Trouble Maker" 是 "Trouble Finder" 左子树的右子树，所以这种操作称为 LR Rotation。同时，这种操作可以看作是两个单旋的组合，称为双旋（Double Rotation）。

同理，也有 RL Rotation，不再赘述。

一般化此情况，即为：

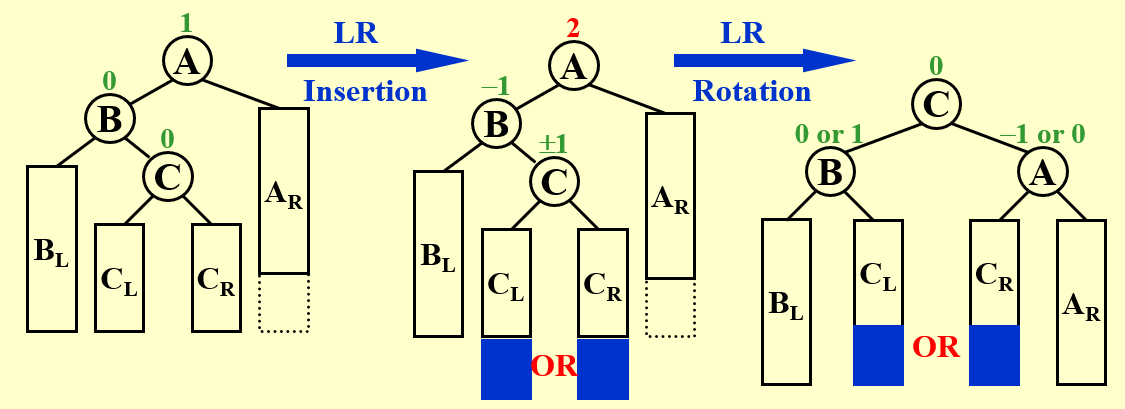
image-20240302133614463

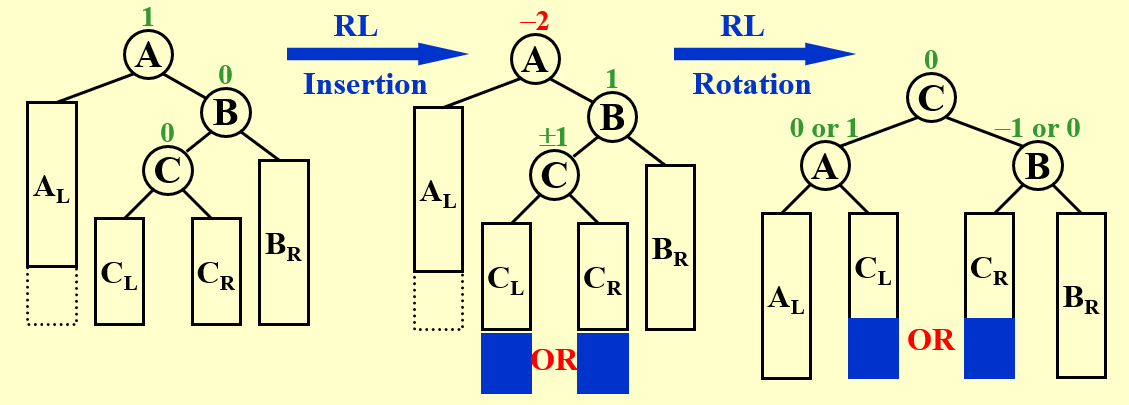
image-20240302133828777

提示

这里的 \(A\) 同样可以不是树根。

1.3 Analysis

二叉搜索树的操作时间复杂度为 \(O(\mathrm{height})\)。这里需要找到这个 height。推导过程如下：

推导过程

记 \(n_{h}\) 为高度为 \(h\) 的平衡二叉树包含最少的结点数。则树的形状必定为：

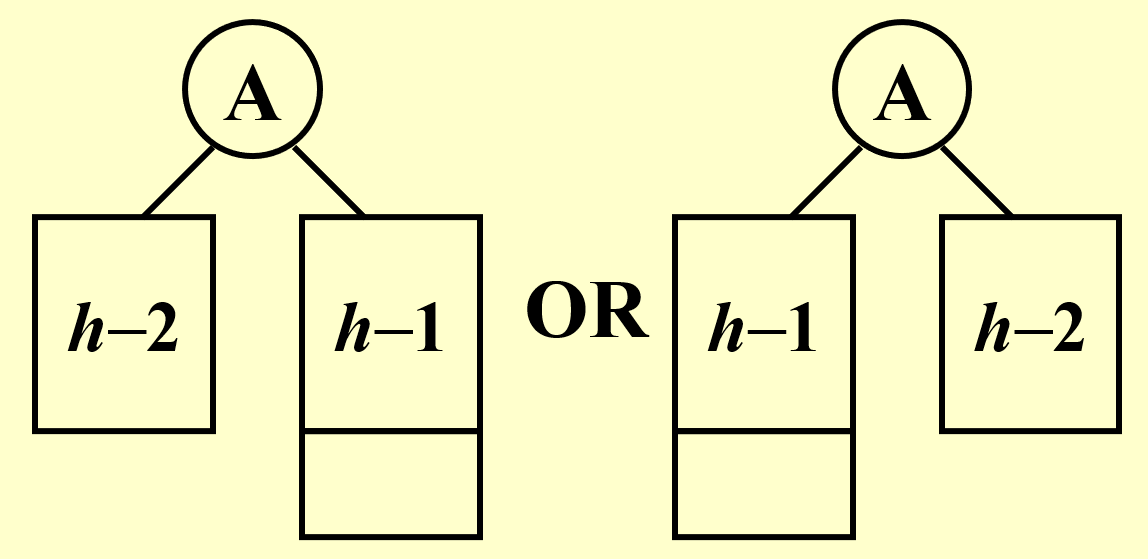
image-20240303153241059

因此推导出 \(n_{h}=n_{h-1}+n_{h-2}+1\)。联想到斐波那契数满足 \(F_{0}=0, F_{1}=1, F_{i}=F_{i-1}+F_{i-2} ,\ \mathrm{for} \ i>1\)，可以证明出 \(n_{h}=F_{h+2}-1, \ \mathrm{for}\ h\ge0\).

由于斐波那契数定理给出了 \(F_{i}\approx \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^{i}\)，因此可以得到\(n_{h}\approx \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^{h+2}-1\)，也就是 \(h\approx O(\mathrm{ln}\ n)\).

2 Splay Trees

  • Target: Any \(M\) consecutive tree operations starting from an empty tree take at most \(O(MlogN)\) time. That means the amortized time(摊还时间) is \(O(logN)\).

提示

AVL 树就是一种伸展树。

注意

摊还时间为 \(O(logN)\)，意味着相较于 AVL 树（任何操作时间都为 \(O(logN)\)），时间上界要求变低了，变成了 \(O(N)\)。但虽然如此，平均效果是差不多的。即使单个操作可能坏到 \(O(N)\)，总用时还是会以 \(O(MlogN)\) 的形式出现。

注意到如果以同样的线性时间方式访问某个节点 \(M\) 次，总用时就有可能变成 \(O(MN)\)，这是我们不想看到的结果。因此采用方法：Whenever a node is accessed, it must be moved.

  • Idea: After a node is accessed, it is pushed to the root by a series of AVL tree rotations.

旋转方法如下：

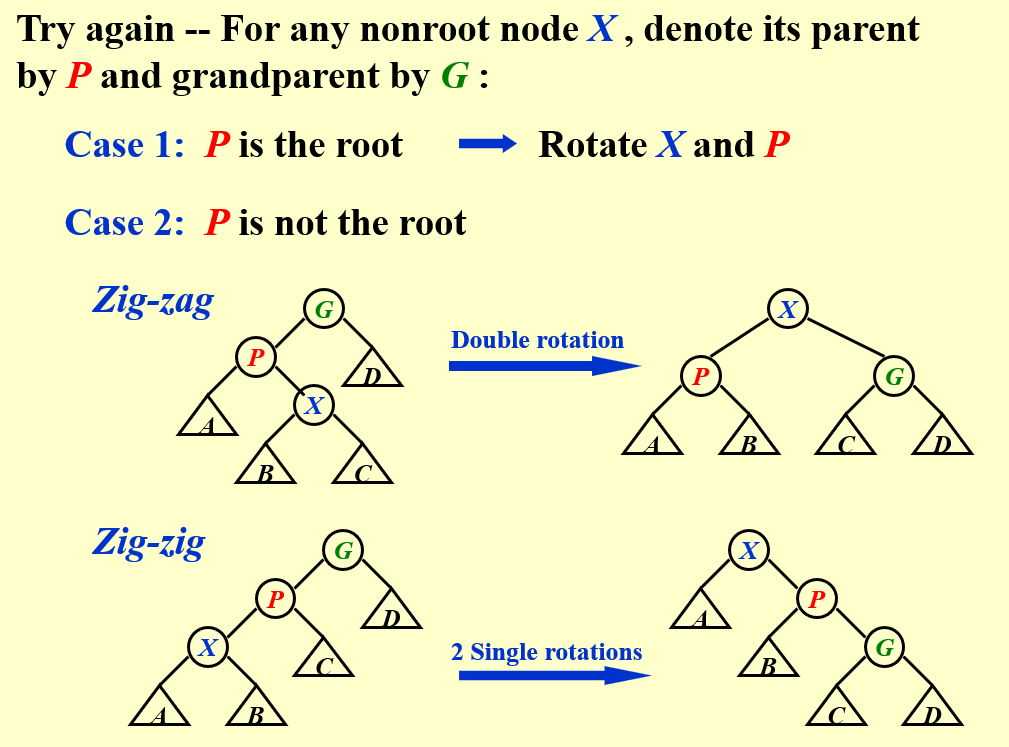
image-20240303134048825

对于删除，分以下步骤进行：

  1. Find X, and X will be at the root;
  2. Remove X, and there will be 2 subtrees \(T_{L}\) and \(T_{R}\);
  3. FindMax(\(T_{L}\)), the largest element will be the root of \(T_{L}\), and has no right child;
  4. Make \(T_{R}\) the right child of the root of \(T_{L}\).

Splay 树实现起来比 AVL 树要简单。

3 Amortized Analysis

  • Target: Any \(M\) consecutive operations take at most \(O(MlogN)\) time. 平均下来每个操作花费时间为 \(O(logN)\)，这称为摊还时间上界（amortized time bound）。

三种时间的比较

worst-case bound >= amortized bound >= average-case bound

Amortized bound does not involve probability. 分析平均情况时也许会假设不同样例之间的概率大小，但是摊还上界都是所有情况的真实平均值。

做摊还分析有三种方法：总量分析、会计法和势能法。

3.1 Aggregate Analysis

总量分析。

  • Idea: Show that for all \(n\), a sequence of \(n\) operations takes worst-case time \(T(n)\) in total. In the worst case, the average cost, or amortized cost, per operation is therefore \(T(n)/n\). 试图证明对所有的 \(n\)，考虑一系列的 \(n\) 个操作，无论这些操作是什么，得到一个最坏情况下的总时间 \(T(n)\)（总量），进而除以 \(n\) 得到摊还开销。

举个栗子

定义堆栈从空栈开始的三种操作：push，pop 和 multipop，其中 multipop 是一次弹出 k 个元素。现在对这些操作的时间进行摊还分析。

push 和 pop 一次的时间都是 \(O(1)\)，而 multipop 一次的时间取决于 k，最大能够到 \(O(n)\)。

我们进行 \(n\) 次操作，假设每次都是 multipop，而且每次 multipop 的时间复杂度都取 \(O(n)\)，看上去总的时间是 \(O(n^2)\)。但是，由于这里是从空栈开始，一个元素压一次不可能弹出来两次，所以上述情况不会发生。

我们可以用 \(n-1\) 次的 push 配合上 \(1\) 次的 multipop，一次弹出 \(n-1\) 个元素，那么总时间就是 \(2n-2\)，进而得到摊还时间就是 \(O(1)\)。

3.2 Accounting Method

会计法。

  • Idea: When an operation’s amortized cost \(\hat{c}_{i}\) exceeds its actual cost \(c_{i}\) , we assign the difference to specific objects in the data structure as credit. Credit can help pay for later operations whose amortized cost is less than their actual cost.

对于所有的 \(n\) 次操作，必须保证 \(\sum\limits_{i=1}^{n}\hat{c}_i\ge\sum\limits_{i=1}^{n}c_i\)。

举个栗子

image-20240303150731349

会计法和总量分析的不同：对于会计法，不同操作的摊还开销可能是不同的（给不同的操作分配不同的 credits）。

对于复杂的问题，想要定下来一个 credits 还是很难的。

3.3 Potential Method

势能法。

  • Idea: \(\hat{c}_i-c_i=Credit_i=\Phi(D_i)-\Phi(D_{i-1})\), where \(\Phi(x)\) is called the Potential function. Sum them up and we get \(\sum\limits_{i=1}^n\hat{c}_i=(\sum\limits_{i=1}^nc_i)+\Phi(D_n)-\Phi(D_0)\).

如果能保证 \(\Phi(D_n)-\Phi(D_0) \ge 0\)，就能确保摊还总开销是实际开销的上界。

问题转变为选取一个好的势能函数。

In general, a good potential function should always assume its minimum at the start of the sequence.

举个栗子

image-20240303151924010

用势能法分析 Splay 树：

这里的势能函数取 \(\Phi(D_{i})=\sum\limits_{i=1}^nlogS(i)\)，其中 \(S(i)\) 是 \(i\) 结点的子孙数量。

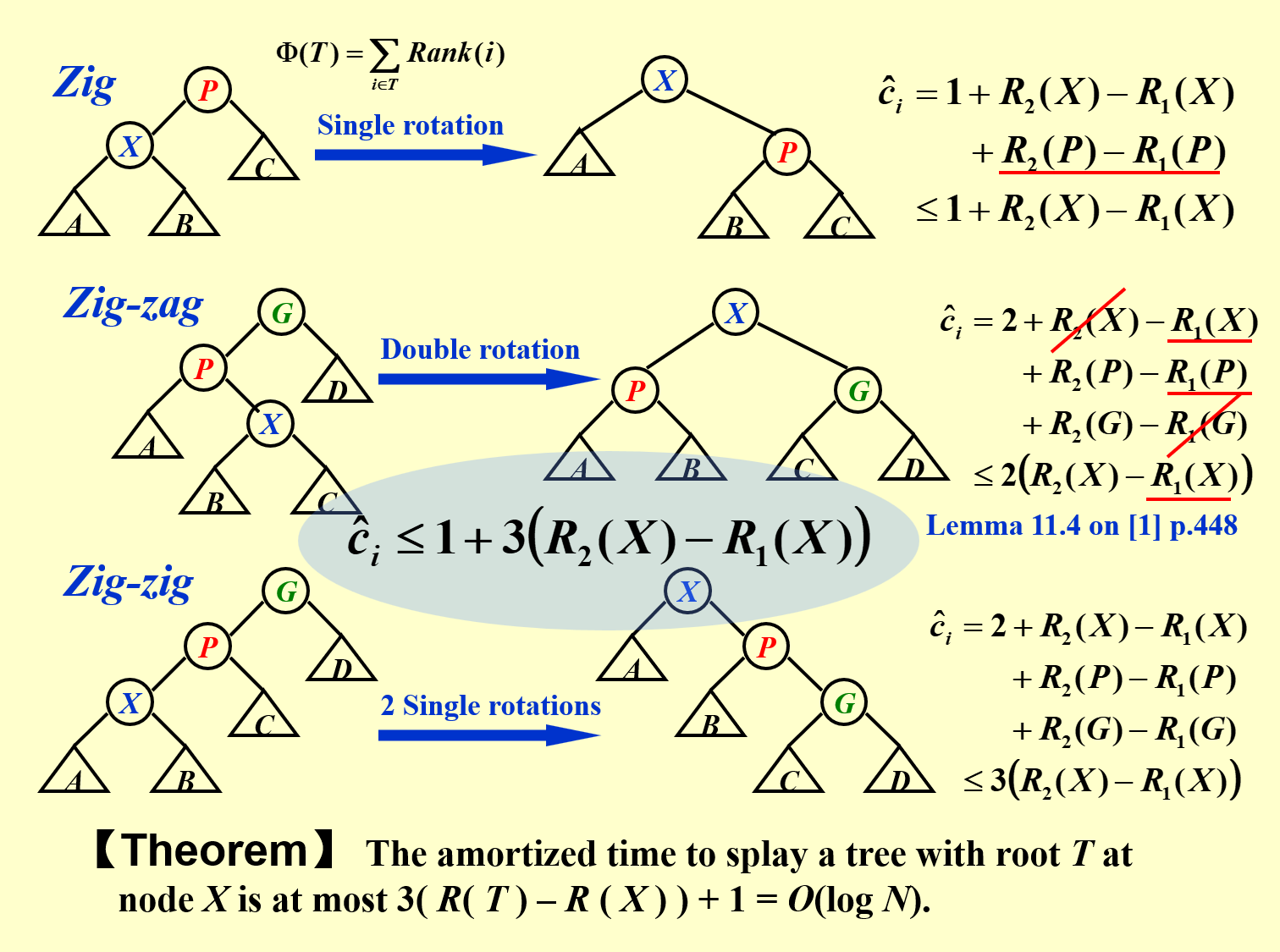
image-20240303152729146

如果操作从空树开始，摊还分析中能够让 \(M\) 较大。如果非空树开始，需要有 \(M\) 充分大的假设，这样才能保证摊还时间上界为 \(O(MlogN)\)。

评论