跳转至

Lecture 11: Approximation

近似算法。

为了解决 NPC 问题，我们有几种角度：

  • 如果 \(N\) 很小，小到 \(O(2^N)\) 也是可以接受的，那么我们可以穷举
  • 可以在某些特定的 special cases 下用多项式时间算法解决
  • 在多项式时间内得到一个接近最优解的解，这就是近似算法

需要注意的是，与贪婪等启发式算法不同的是，贪婪是不管效果的，而近似算法会有近似解的质量方面的讨论。

1 Approximation Ratio

对于任意的输入大小 N，我们记近似算法的解为 \(C\)，最优解为 \(C^*\)，那么我们定义近似比例（Approximation Ratio）\(\rho(n)\) 为满足如下条件的值：

\[ max(\frac{C}{C^*}, \frac{C^*}{C}) \le \rho(n) \]

这里有两项的 max 代表我们需要考虑最大化问题和最小化问题。

还有关于 approximation scheme 的概念，即对于任意的 \(\epsilon > 0\)，我们可以在得到一个解，其近似比例为 \(1 + \epsilon\)。

我们称一个 approximation scheme 是 polynomial-time approximation scheme（PTAS）如果其运行时间关于 N 是多项式的，例如 \(O(N^{2/\epsilon})\)。

我们称一个 approximation scheme 是 fully polynomial-time approximation scheme（FPTAS）如果其运行时间关于 1/epsilon 和 N 是多项式的，例如 \(O((1/\epsilon)^2n^3)\)。

2 Example: Bin Packing

原问题是一个 NP Hard 问题，它的 decision version 是 NP Complete。

解决这个问题有以下几种方法：

2.1 Next Fit

按照顺序读 item，如果独到的 item 在当前的 bin 放得下就装，否则为 item2 开一个新的 bin。

近似比？记最优解需要的 bin 数量为 M，则 next fit 的解需要不超过 2M-1 个 bin，并且存在一个序列使得 next fit 的解恰好是 2M-1 个 bin。近似比为 2。

2.2 First Fit

读到 item 的时候，寻找第一个能放下 item 的 bin，如果没有就开一个新的 bin。

近似比？记最优解需要的 bin 数量为 M，则 first fit 的解需要不超过 17M/10 个 bin，并且存在一个序列使得 first fit 的解恰好是 17(M-1)/10 个 bin。近似比为 1.7。

2.3 Best Fit

读到 item 的时候，寻找能装下、且装下 item 之后剩余空间最小的 bin，否则就开一个新的 bin。

近似比？也是 1.7。

此外还有 worst fit（装最不满的）、almost worst fit、any fit 等。都是 1.7。

上面三个都是 online algorithms，即只能读到 item 之后才能决定放在哪个 bin。

定理

存在输入序列使得任意的 online 的集装箱问题使用的数量至少是最优解数量的 5/3 倍。

2.4 Offline Algorithm: First Fit Decreasing

先把 size 按照递减顺序排序，然后用 first fit 或者 best fit。

定理

First Fit Decreasing 使用不超过 11M/9+6/9 个 bin，其中 M 是最优解的 bin 数量。且存在一个序列使得 First Fit Decreasing 的解是 11M/9+6/9 个 bin。

这时简单的贪婪启发算法也能给出较好的结果。

3 Example: The KnapSack Problem

背包问题。

对于可以分割的版本，我们可以使用贪心算法，贪心的条件是选择 profit/weight 最大的 item。

对于 0-1 背包问题（这是一个 NP-Hard 问题），贪婪不一定得到最优解。如果我们使用最大价值或者最大性价比的 item，那么贪心算法的近似比是 2。证明如下：

a0bfb8dc04996851308fc7ae7283991c

0-1 背包问题还能使用动态规划来解决。我们记 \(W_{i,p}\) 是从前 \(i\) 个 item 中选出的 profit 恰好为 \(p\) 的最小 weight。那么我们有如下的递推关系：

\[ W_{i,p} = \left \{ \begin{aligned} & \infty & \text{if } i=0 \\ & W_{i-1,p} & \text{if } p_i > p \\ & min(W_{i-1,p}, W_{i-1,p-p_i}+w_i) & \text{otherwise} \end{aligned} \right. \]

这里的 i 从 1 到 n，p 从 1 到 \(np_{max}\)。时间复杂度为 \(O(n^2p_{max})\)。

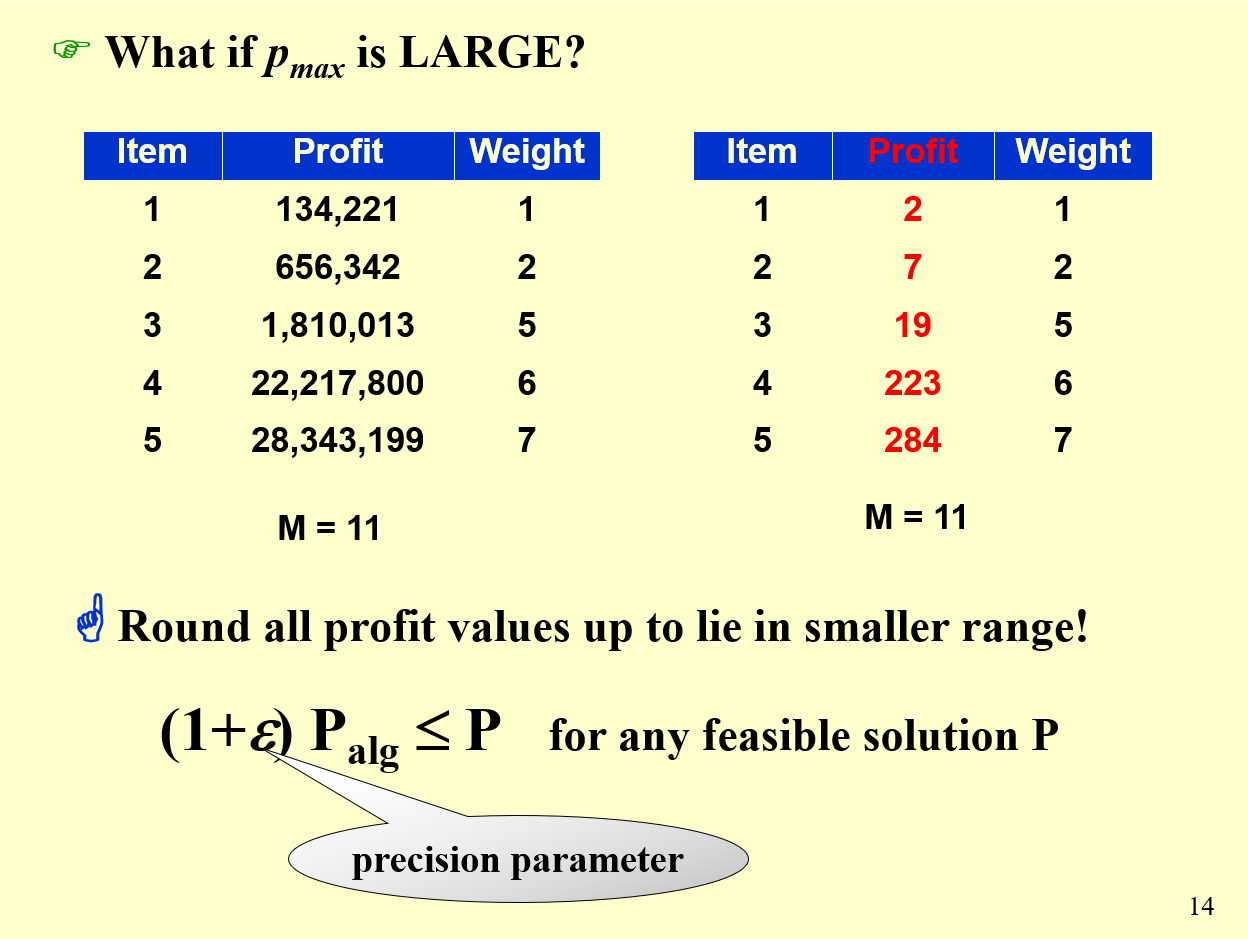
需要注意的是这里的时间复杂度中 input size 包括 pmax 的二进制编码长度 d，所以 pmax 是指数级别的，这个算法并不是多项式时间的。

那如果 pmax 很大咋办呢？我们把 profit 通过除以某一个数字进行缩放，然后再进行动态规划。

328e481fe247e77e4b77cfddda1c31ae

4 Example: The K-Center Problem

最简单的贪心算法，我们从第一个 center 开始，每次添加 center 来减小 covering radius。

这很不好。

改进：Greedy-2r，每次添加一个 center，然后把所有的点都 cover 住。

如果 r 是一个整数，则时间复杂度是 \(O(\log r)\)。

定理

Unless P = NP, there is no \(\rho\)-approximation algorithm for the k-center problem with \(\rho < 2\).

5 Summary

  • A: Optimality
  • B: Efficiency
  • C: All instances

Even if P = NP, still we cannot guarantee A+B+C.

评论