Lecture 12: Local Search¶
局部搜索。
1 Framework of Local Search¶
- Local: Define a neighborhood of solutions, find a local optimum.
- Search: Start with a feasible solution and search a better one within the neighborhood. A local optimum is achieved if no improving solution can be found.
2 Example: Vertex Cover¶
- Feasible solution: all the vertex covers.
- Search: Start from S = V, delete a node and check if S' is a vertex cover with a smaller size.
有几种情况:
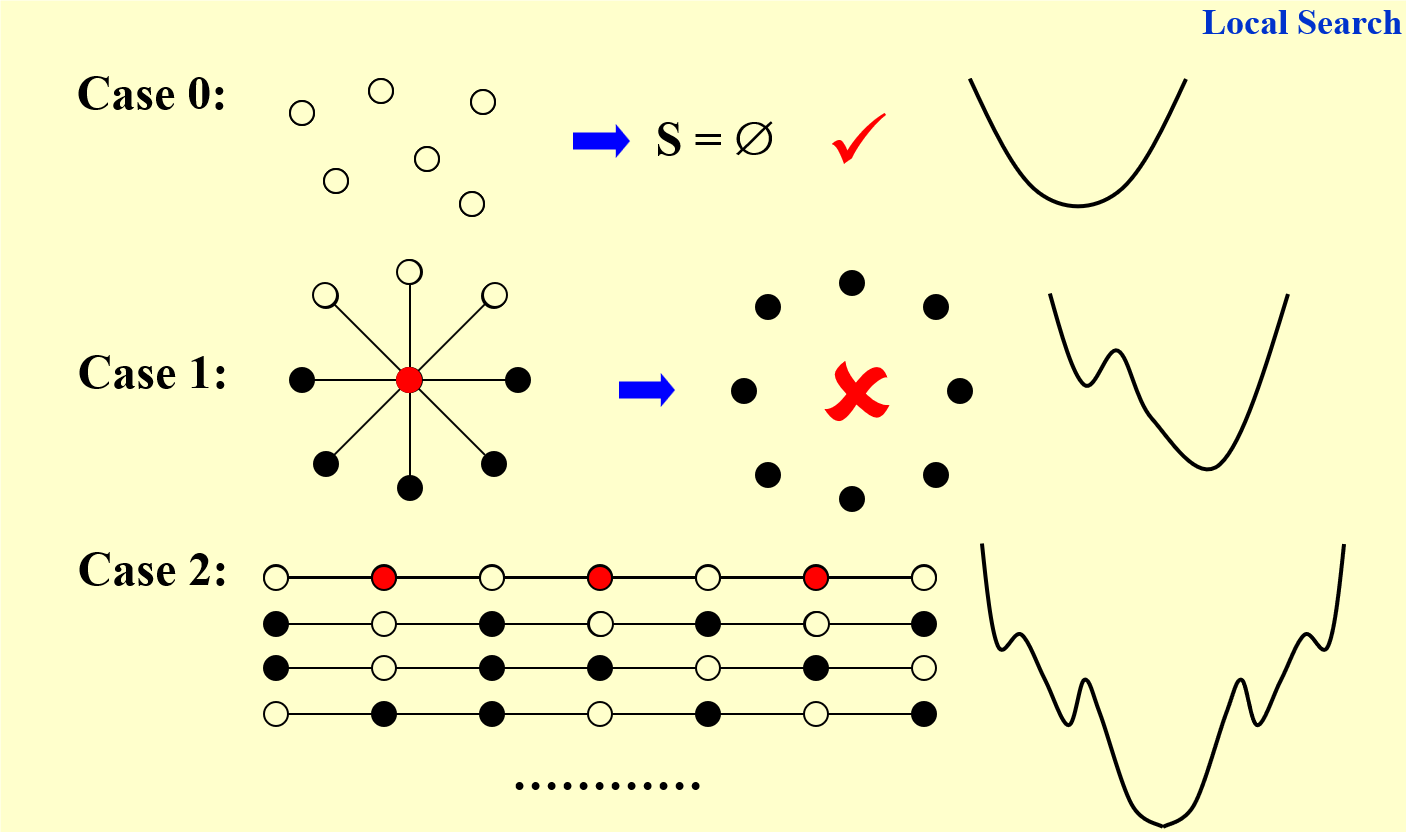
为了防止我们一开始就把最优解的点去掉(并且是不能 undo 的),我们可以使用 The Metropolis Algorithm。
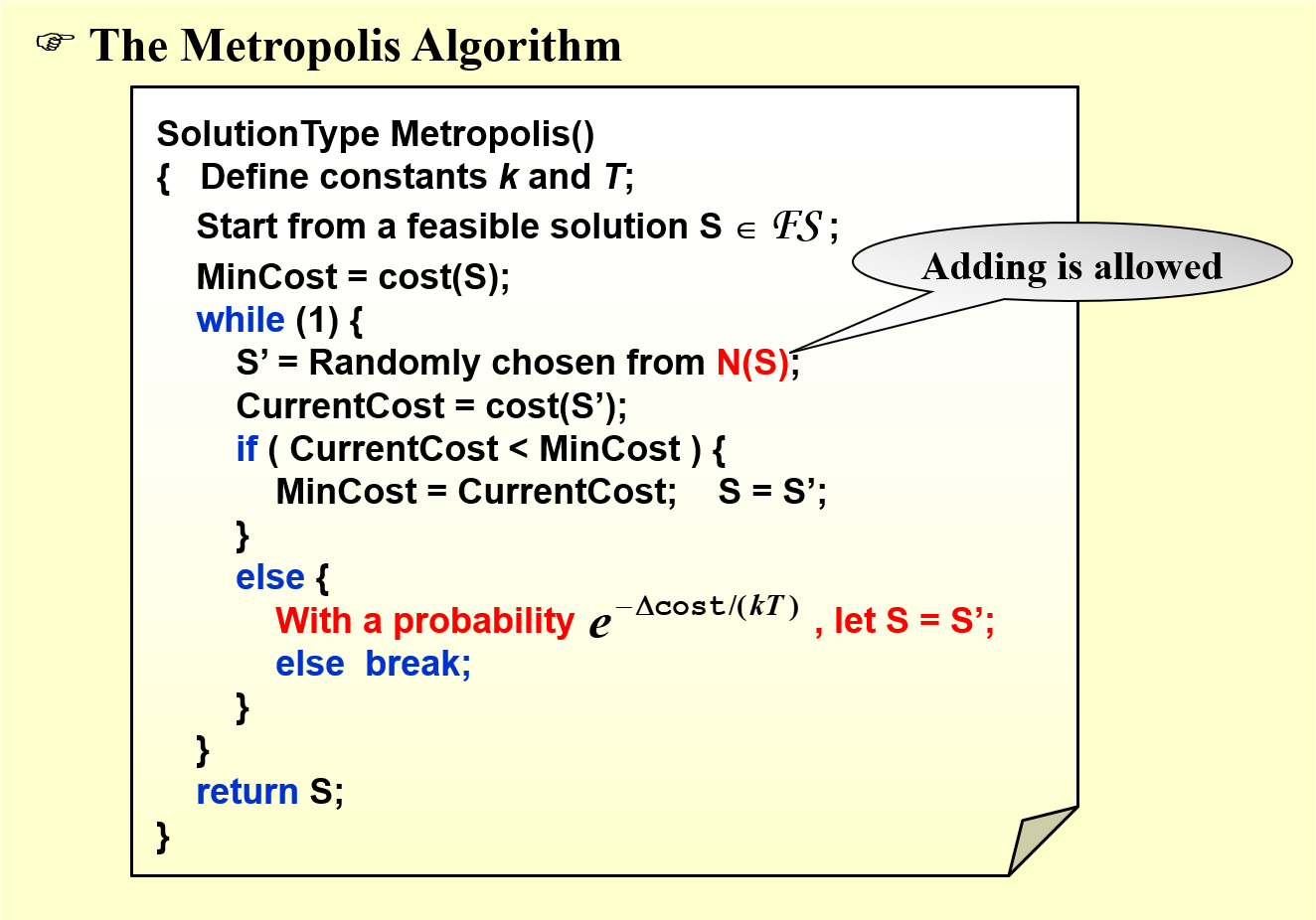
这里面的概率和定义的温度 T 有关系。当 T 很高的时候,上坡的概率几乎为 1,容易引起底部震荡;当 T 很低的时候,上坡的概率几乎为 0,接近原始的梯度下降法。
对于 case 1,有一定概率可以跳出 local optimum 得到正确解。但是对 case 0,有可能在加 1 和减 1 之间无限震荡。
为此,我们需要实现 Simulated Annealing,即模拟退火:制定一个 cooling schedule,逐渐降低温度,使得概率逐渐变小。
3 Example: Hopfield Neural Network¶
这个问题有几个定义需要注意:
- 边权重为负,表示不同的节点之间是 same state;边权重为正,表示不同的节点之间是 different state。
- 有可能不存在一个使得所有边都满足这个条件的 configuration。
- 对于边来说,符合上面这个规则就称为 good,否则称为 bad。
- 对于结点来说,如果所有与它相连的边的 \(w_e s_u s_v\) 加起来是小于 0 的,就称这个节点是 satisfied 的,否则是 unsatisfied 的。
- 如果这个图的所有节点都是 satisfied 的,就称这个图是 stable 的。
问题来了。这个问题中的网络是否总有一个 stable 的状态呢?如果有,如何找到这个 stable 的状态呢?
答案是有的。我们可以使用一个非常简单的 state-flipping algorithm:从任意一个 configuration 开始,如果它不是 stable 的,就选择一个 unsatisfied 的节点,然后 flip 它的状态。
这个算法会在最多 \(W=\sum_e|w_e|\) 次循环后终止到 stable 状态。
用局部搜索的思想来思考这个问题:
- Feasible solution: 任意一个 configuration。
- Search: 从任意一个 configuration 开始,如果它不是 stable 的,就选择一个 unsatisfied 的节点,然后 flip 它的状态。
Any local maximum in the state-flipping algorithm to maximize is a stable configuration.
是否是多项式时间?有待研究。
4 Example: The Maximum Cut Problem¶
图分为两组顶点,要求跨组的所有边权重之和最大。
局部搜索思考:
- Feasible Solution: 任意一个分割
- Search: 把一个顶点从 B 移到 A,或者反过来。
实际上是上面问题的一种特例:边权重都为正值。
问题:这个局部最优解有多好?
答案:\(w(A,B) \ge 1/2w(A^*,B^*)\).
Unless P = NP, no 17/16 approximation algorithm for max-cut.
由于这个算法可能不在多项式时间内完成,我们想让他在“没有重大提升”的时候就停下来,为此,定义
Big-improvement-flip: Only choose a node which, when flipped, increases the cut value by at least
定义这种翻转之后,我们可以得到其近似比为 2+\(\epsilon\),而且最多在 \(O(n/\epsilon \log W)\) 次翻转之后就结束。