Lecture 2: Red-Black Trees and B+ Trees¶
红黑树和 B+ 树。
前面的 AVL 树对【平衡】这个概念的定义是任意节点左子树高度与右子树高度最多相差1,我们得到这样的树高确实是 \(O(logN)\) 级别的。
但是对搜索树的平衡定义可以不尽相同,例如这一讲的红黑树和 B+ 树也是平衡的,而且在实际系统中更加常用。
1 Red-Black Trees: Definition¶
- Target: Balanced binary search tree
红黑树的结点示意图如下。NIL(空结点)一般称为外点。
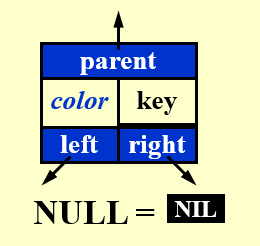
A red-black tree is a binary search tree that satisfies the following properties:
- Every node is either red or black.
- The root is black.
- Every leaf (NIL) is black.
- If a node is red, then both its children are black.
- For each node, all simple paths from the node to decendant leaves contain the same number of black nodes.
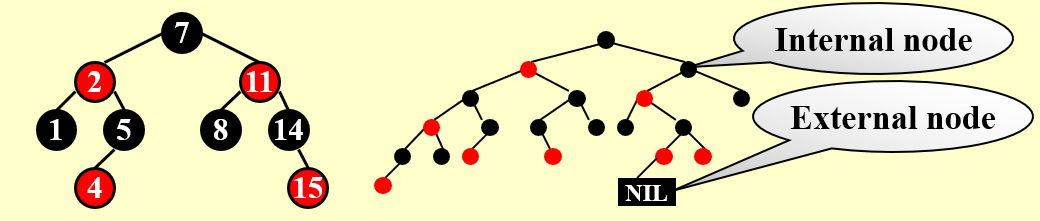
Black-Height 的定义
The black-height of any node x, denoted by bh(x), is the number of black nodes on any simple path from x (x not included) down to a leaf. bh(Tree)=bh(root).
Lemma
A red-black tree with \(N\) internal nodes has height at most \(2ln(N+1)\).
2 Red-Black Trees: Operations¶
2.1 Insertion¶
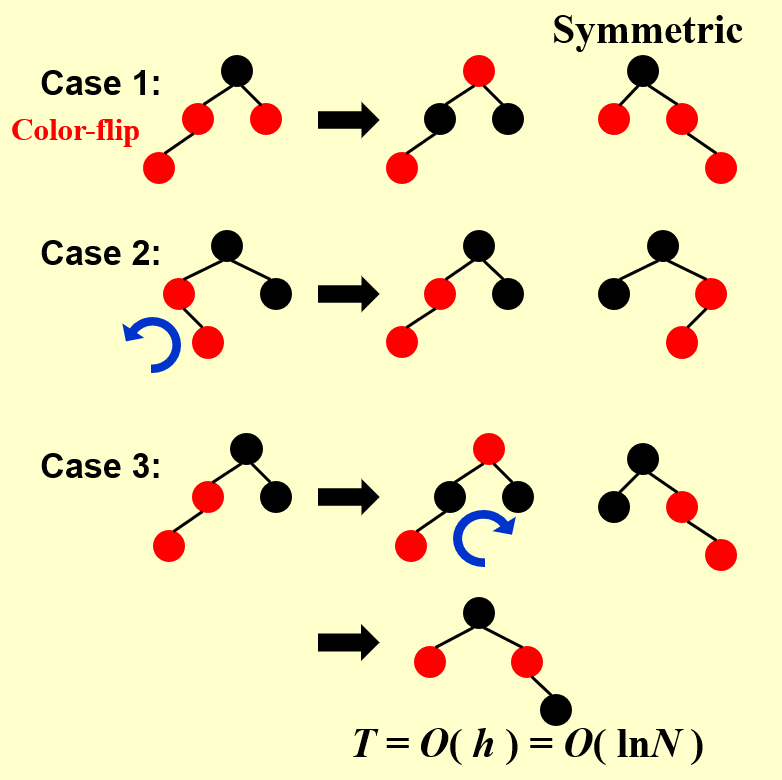
- Idea: Insert & color red.
2.2 Deletion¶
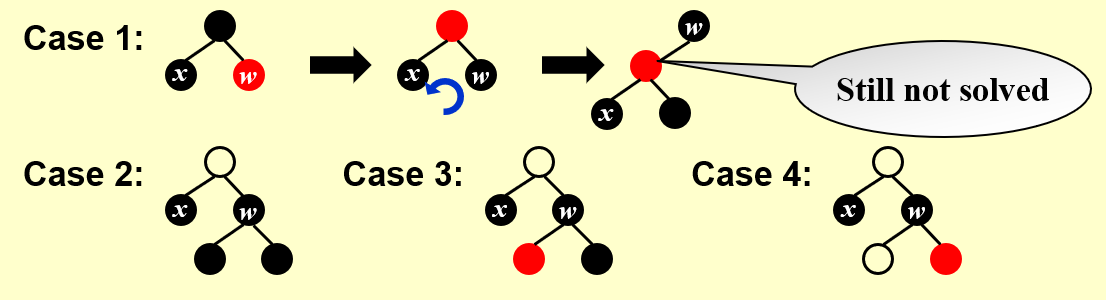
尽量不改变结点的颜色。最多只需要三次操作就可以实现,这是相对于 AVL 树的优势。
唯一需要重新平衡的时候就是删除一个黑色叶节点。由于需要保持平衡,我们需要在这条路径上加一个黑色结点。
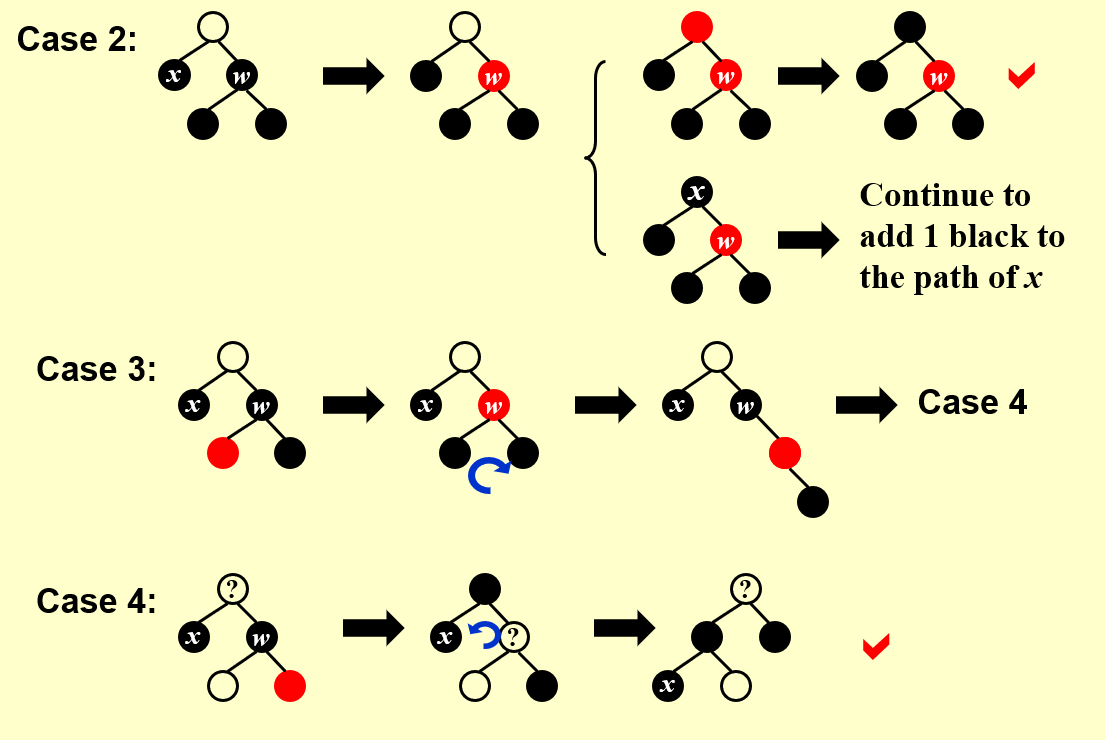
3 Comparison with AVL Trees¶
Number of rotations:
| AVL Tree | Red-Black Tree | |
|---|---|---|
| Insertion | \(\le2\) | \(\le2\) |
| Deletion | \(O(logN)\) | \(\le3\) |
4 B+ Trees¶
定义:
A B+ Tree of order M is a tree with the following structural properties:
- The root is either a leaf or has between 2 and M children.
- All nonleaf nodes (except the root) have between \(\lceil M/2 \rceil\) and M children.
- All leaves are at the same depth.