Lecture 4: Leftist Heaps and Skew Heaps

左式堆与斜堆。

1 Leftist Heap: Definition

在基础课程中已经学习了利用完全二叉树来实现一个优先队列（堆），但是完全二叉树并不是实现堆的唯一方法。

使用完全二叉树来实现一个堆，在插入、删除与查找操作中能得到很好的效率 \(O(logN)\)，但是有时候我们还需要第四种操作，即合并（merging），因此对于左式堆来说：

• Target: Speed merging up to \(O(N)\).

使用完全二叉树类型的堆合并

​最快可以到 \(\Theta(N)\)。我们将两个堆的数组复制下来调用 BuildHeap 操作即可。问题是：它是 \(\Theta(N)\) 而不是 \(O(N)\)，我们希望得到一个更快的方法。如果使用指针来存储堆，将会拖慢每一步的时间。如何抵消这些时间呢？答案是左式堆。

• Order Property: The same.
• Structure Property: Binary trees, but unbalanced.

Null Path Length 的定义

The null path length, Npl(X) of any node X is the length of the shortest path from X to a node without two children. Define Npl(NULL) = -1.

注意这里有 Npl(X) = min { Npl(C) +1 for all C as Children of X }.

左式堆的定义即为：For every node X in the heap, the Npl of the left child is at least as large as that of the right child.

例如：

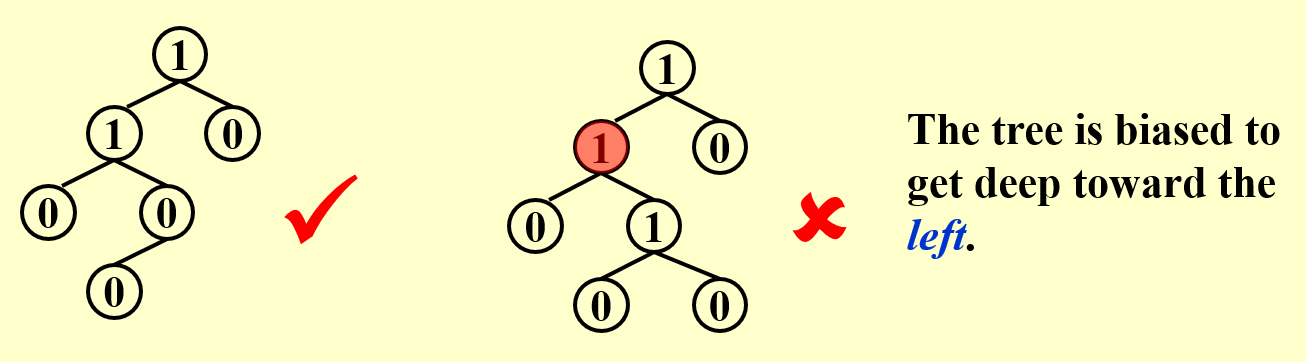
可以看出左式堆有向左倾斜的倾向。

定理

A leftist tree with \(r\) nodes on the right path must have at least \(2^r-1\) nodes.

这个定理告诉我们，一个包含 \(N\) 个结点的左式堆在根节点的右路径最多有 \(\lfloor log(N+1) \rfloor\) 个结点，也即右路径长度为 \(O(logN)\)。我们可以将操作都放到右子树来做。

2 Leftist Heap: Operations

结构定义：

struct TreeNode{
    ElementType Element;
    Heap Left;
    Heap Right;
    int Npl;
}

由于插入可以看作是合并的特例，这里介绍合并的操作：

2.1 Merge (recursive version)

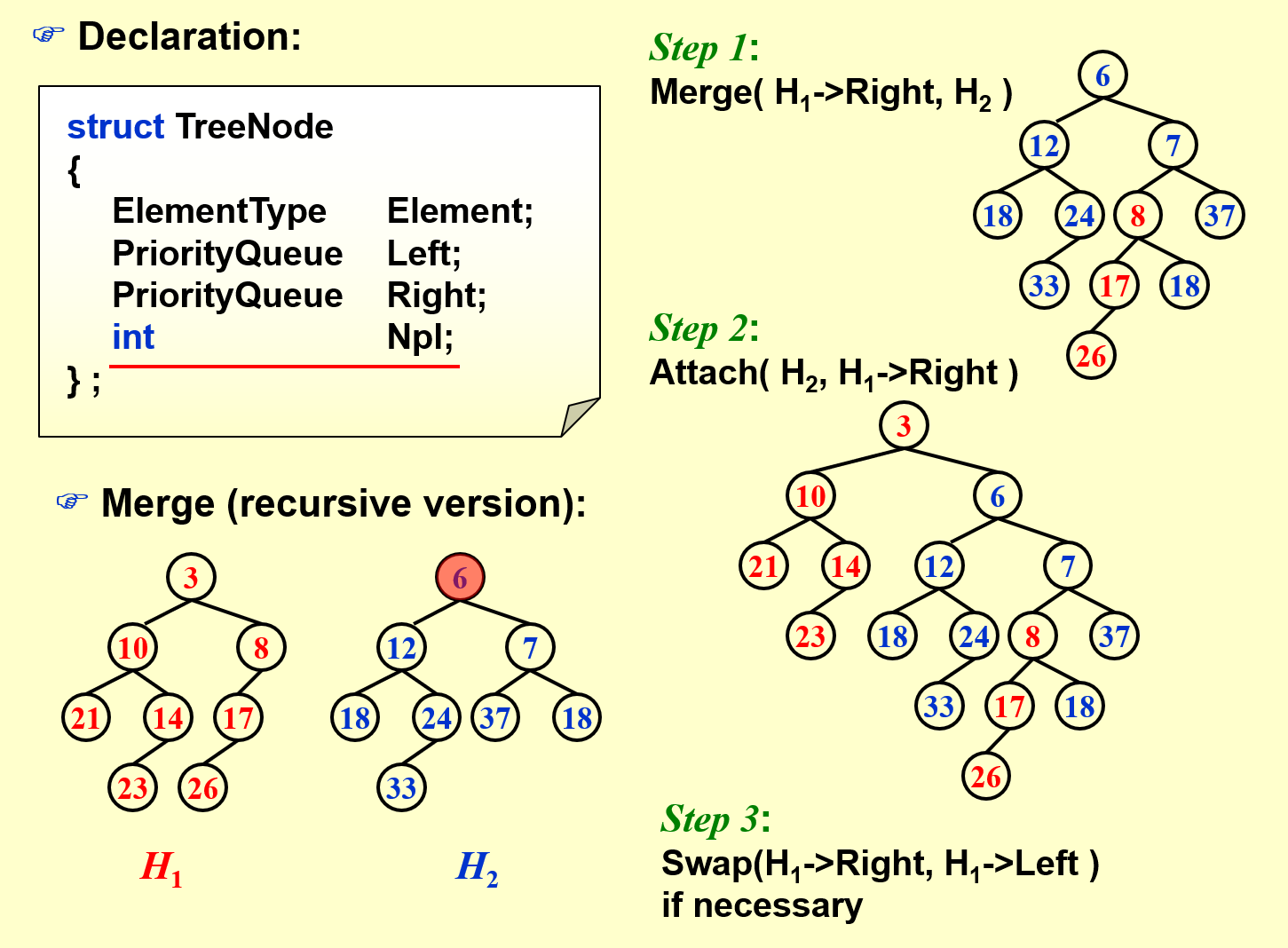
首先比较根节点，保留需要作为根的那个节点（这里是 3），然后将另一个堆与保留节点的右子树进行递归合并，然后合并完成之后 Attach 上去即可。最后需要看一下结果的树，如果不是左式堆则需要根节点左右儿子交换。

上代码：

PriorityQueue  Merge ( PriorityQueue H1, PriorityQueue H2 )
{ 
    if ( H1 == NULL )   return H2;  
    if ( H2 == NULL )   return H1;  
    if ( H1->Element < H2->Element )  return Merge1( H1, H2 );
    else return Merge1( H2, H1 );
}

static PriorityQueue
Merge1( PriorityQueue H1, PriorityQueue H2 )
{ 
    if ( H1->Left == NULL )     /* single node */
        H1->Left = H2;  /* H1->Right is already NULL 
                    and H1->Npl is already 0 */
    else {
        H1->Right = Merge( H1->Right, H2 );     /* Step 1 & 2 */
        if ( H1->Left->Npl < H1->Right->Npl )
            SwapChildren( H1 ); /* Step 3 */
        H1->Npl = H1->Right->Npl + 1;
    } /* end else */
    return H1;
}

\(T_p = O(logN)\).

2.2 Merge (iterative version)

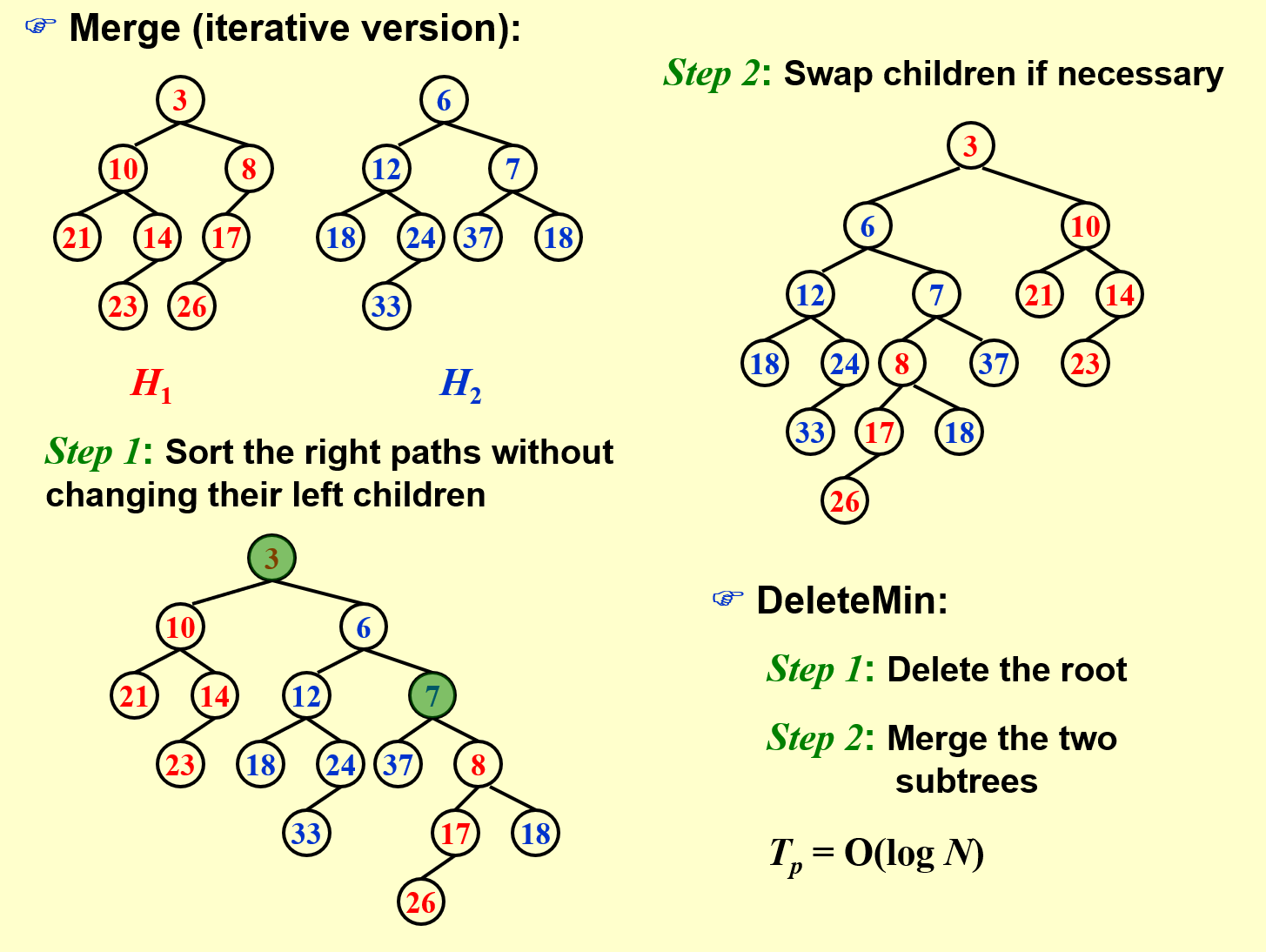
先对两个堆的右路径做类似归并排序的 Merge 操作，然后检查需要更换左右儿子结点的结点并进行更换。这个和前面的递归版本是对等的。

2.3 DeleteMin

如上图。删除根结点之后合并即可。\(O(logN)\).

3 Skew Heap: Definition

它与左式堆的关系就好比伸展树与 AVL 树之间的关系。是一种简化版的左式堆。不关注NPL。

• Target: Any \(M\) consecutive operations take at most \(O(MlogN)\) time.

做法？

Always swap the left and right children excpet that the largest of all the nodes on the right paths does not have its children swapped. NO NPL.

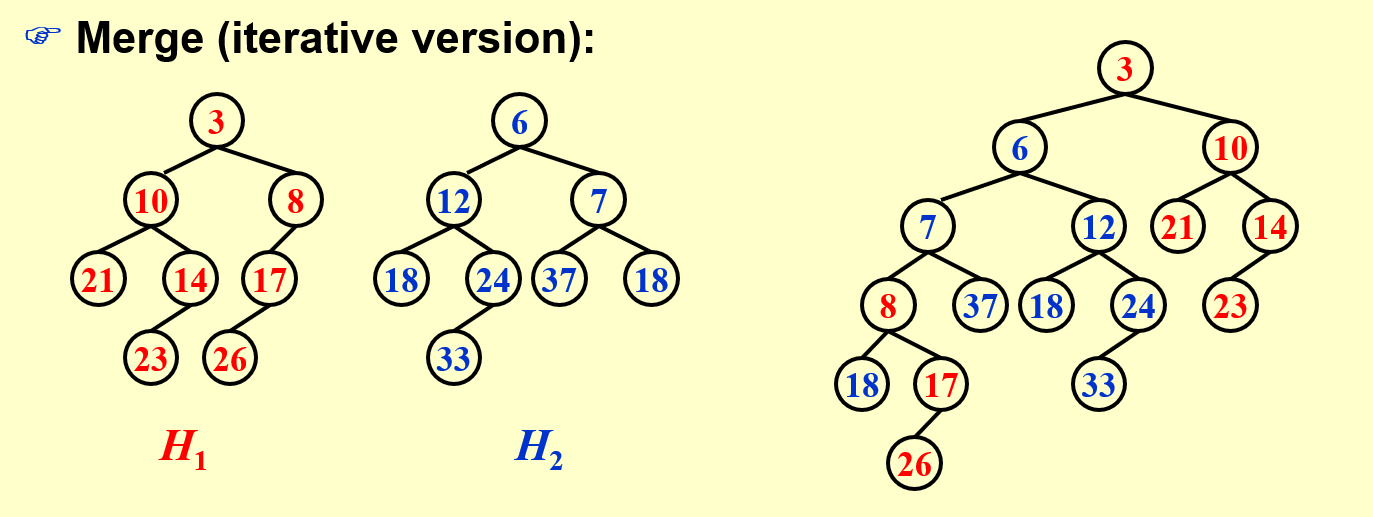
与左式堆类似，需要时刻在右路径上做 merge。但是每 attach 一次之前都交换一次左右儿子。

两点解释

1. 斜堆的好处是不需要使用记录 npl 的额外空间，而且无需 if-else 判断；
2. 对于斜堆和左式堆，我们都不知道精确的右路径长度。

4 Skew Heap: Analysis

证明：斜堆的摊还时间操作为 \(O(logN)\).

Heavy node 的定义

A node \(p\) is heavy if the number of the descendants of \(p\)'s right subtree is at least half of the number of descendants of \(p\), and light otherwise. Note the descendants of \(p\) includes \(p\) itself.

也就是说某个节点的右子树结点总数至少是该结点所有后代（加上它自己）数量的一半，就叫 heavy node。

这里的势能函数就取作 \(\Phi(D_i) = \mathrm{number\ of\ heavy\ nodes}\).

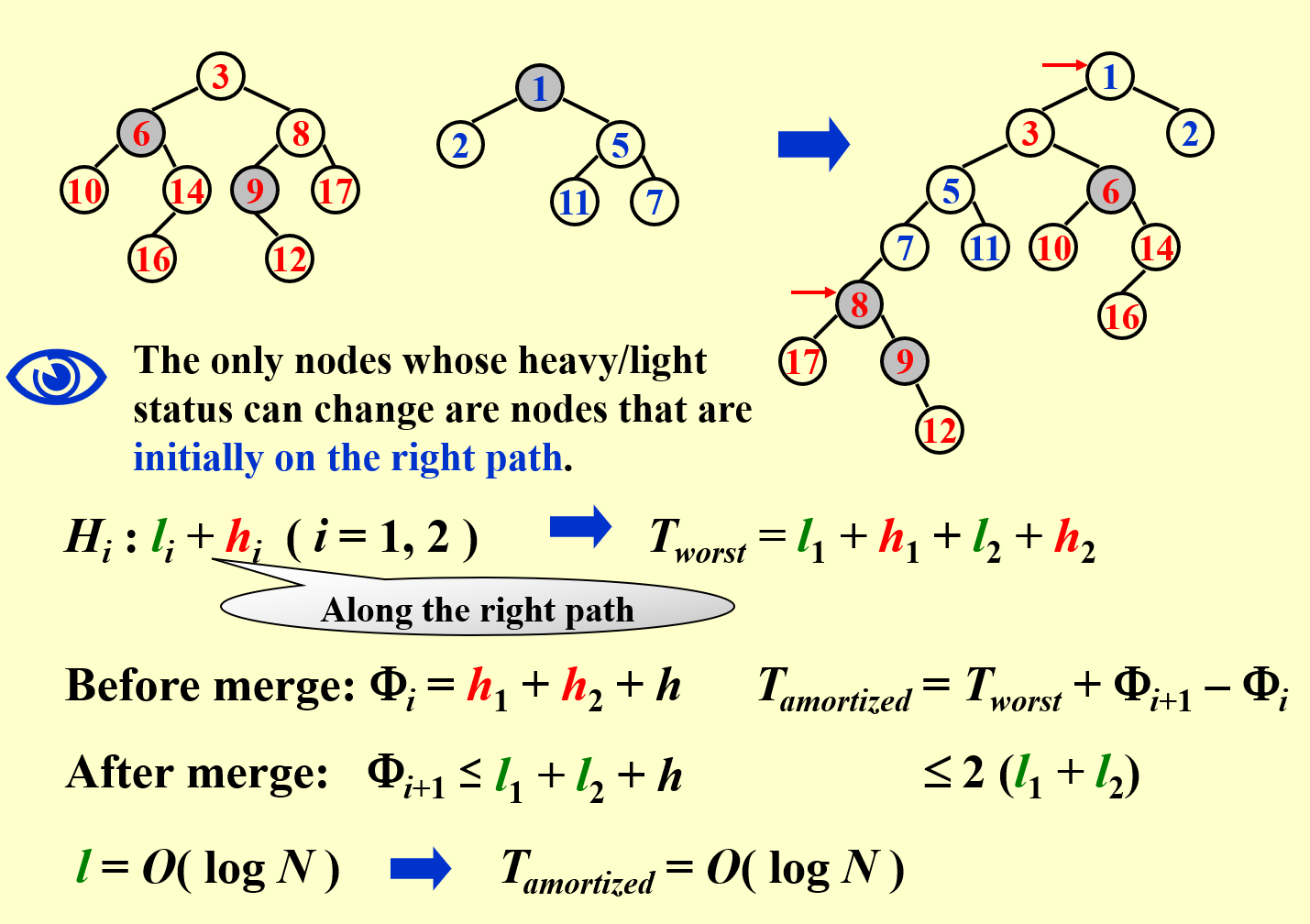
注意观察到合并前右路径上的 heavy node 将全部变为 light node，而部分 light node 将会变为 heavy node，这里取最坏情况。最终得到摊还时间为 \(O(logN)\)。

评论