跳转至

Lecture 6: Backtracking

回溯算法。

1 Introduction

回溯算法的目的，或者说来源？

对于一般的问题我们可能想到的是暴力枚举。这在结果为有限集的时候确实是能够保证得到正确答案的，但是其速度较慢，而且在结果为无限集的时候会出现问题。

回溯算法能够让我们从大的解集中进行剪枝（pruning），而依然保证我们能够得到正确的答案。这种方法能够让我们在比较早的时候就知道某一个区域的解集是不会正确的，从而不访问那些答案。

其基本思想是在一个部分正确的解集 \((x_1, x_2, ..., x_i)\) 中添加一个新的 \(x_{i+1}\)，然后看是否正确。如果正确的话就继续，如果不正确就把 \(x_{i}\) 删掉，也就是回退到上一个解 \((x_1, x_2, ..., x_{i-1})\)。

2 Example: Eight Queens

基本问题就是在 8*8 的棋盘中放置八个棋子，要求两两之间满足：不在同一行、不在同一列而且不在同一对角线。

在这一种问题里面我们如何使用回溯算法？分为以下步骤：

  1. 构建 Game Tree。这个游戏树中每一条从根节点道叶子节点的路径就是一个解。
  2. 对这个树进行深度优先搜索（DFS），遇到违反游戏规则的结点就进行剪枝，然后 undo。

注意在实际的程序编写中没有实际构建树，这只是一个抽象的概念。要不然的话跟暴力枚举就没区别了。

3 Example: The Turnpike Reconstruction Problem

问题：Given \(N\) points on the \(x\)-axis with coordinates \(x_1<x_2<...<x_N\). Assume that \(x_1=0\). There are \(N(N-1)/2\) distances between every pair of points.

Now given those \(N(N-1)/2\) distances and reconstruct a point set from the distances.

给出相对距离，求坐标集合。

一个回溯算法的模板：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
bool backtracking(int i)
{
    found = false;
    if(i>n) return true;

    for(each x_i in S_i)
    {
        OK = check((x_1,...,x_i),R);
        if(OK)
        {
            count x_i in;
            found = backtracking(i+1);
            if(!found) undo(i);
        }
        if(found) break;
    }

    return found;
}

关于搜索树的选择：

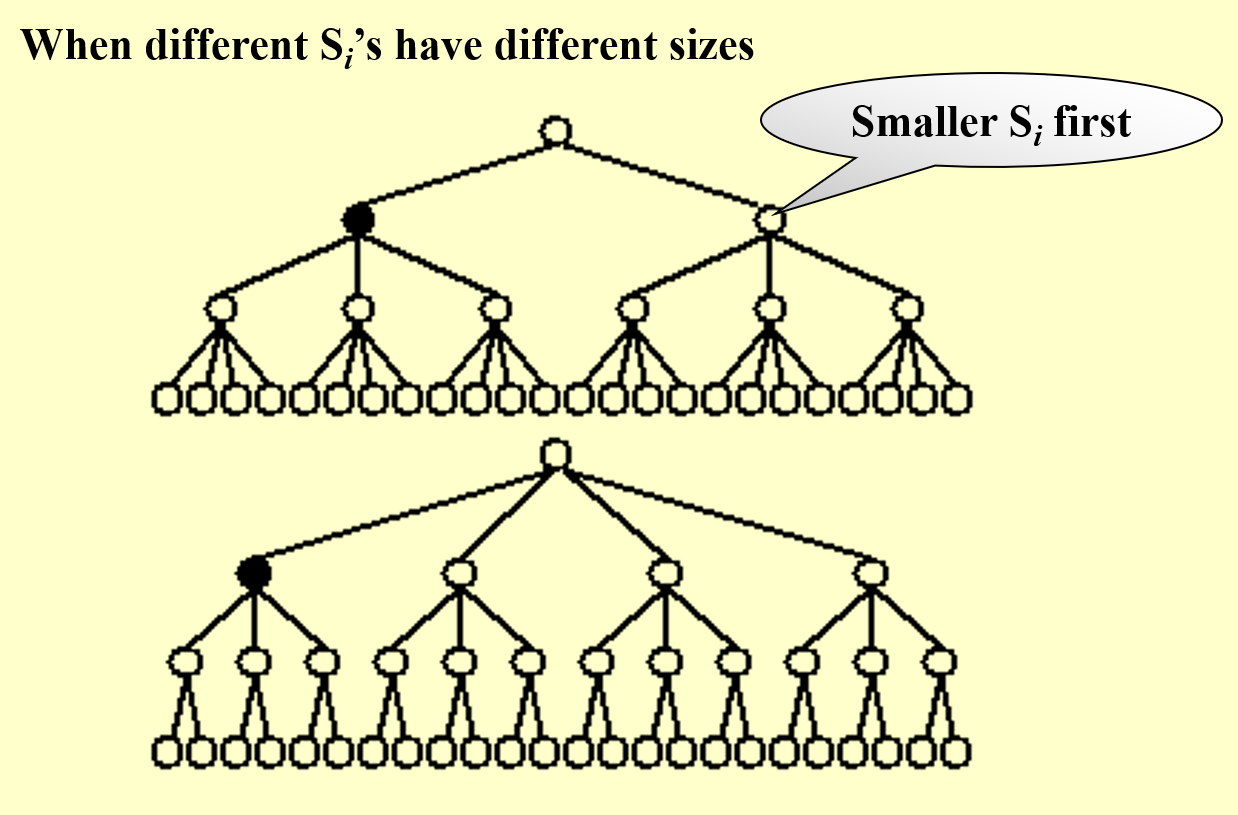
20240406170907

我们一般选择更小规模的树，这样剪枝的时候能够剪更多。

4 Example: Game of Tic-tac-toe

对于五子棋游戏我们同样可以构建游戏树。在计算机进行决策的时候使用暴力枚举法太过于耗时，于是便有以下相关技术：

  1. Minimax 为每一个状态赋一个 "Goodness" 值，例如： $$ f(P) = W_{Computer} - W_{Human} $$ 这里 \(W\) 代表在状态 \(P\) 的时候赢局的种类数。 计算机决策的时候让这个值最大，人决策的时候让这个值最小。

  2. Alpha-beta pruning

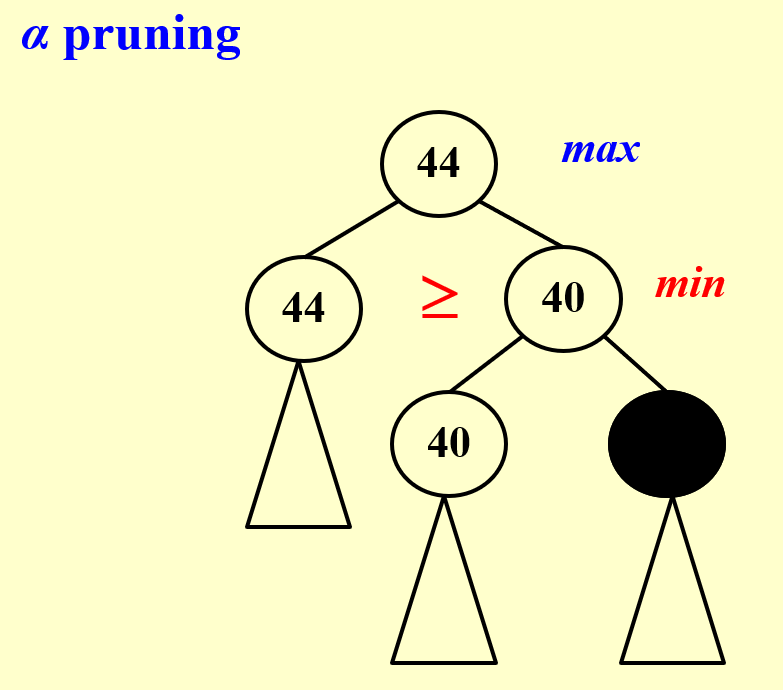
20240406172338

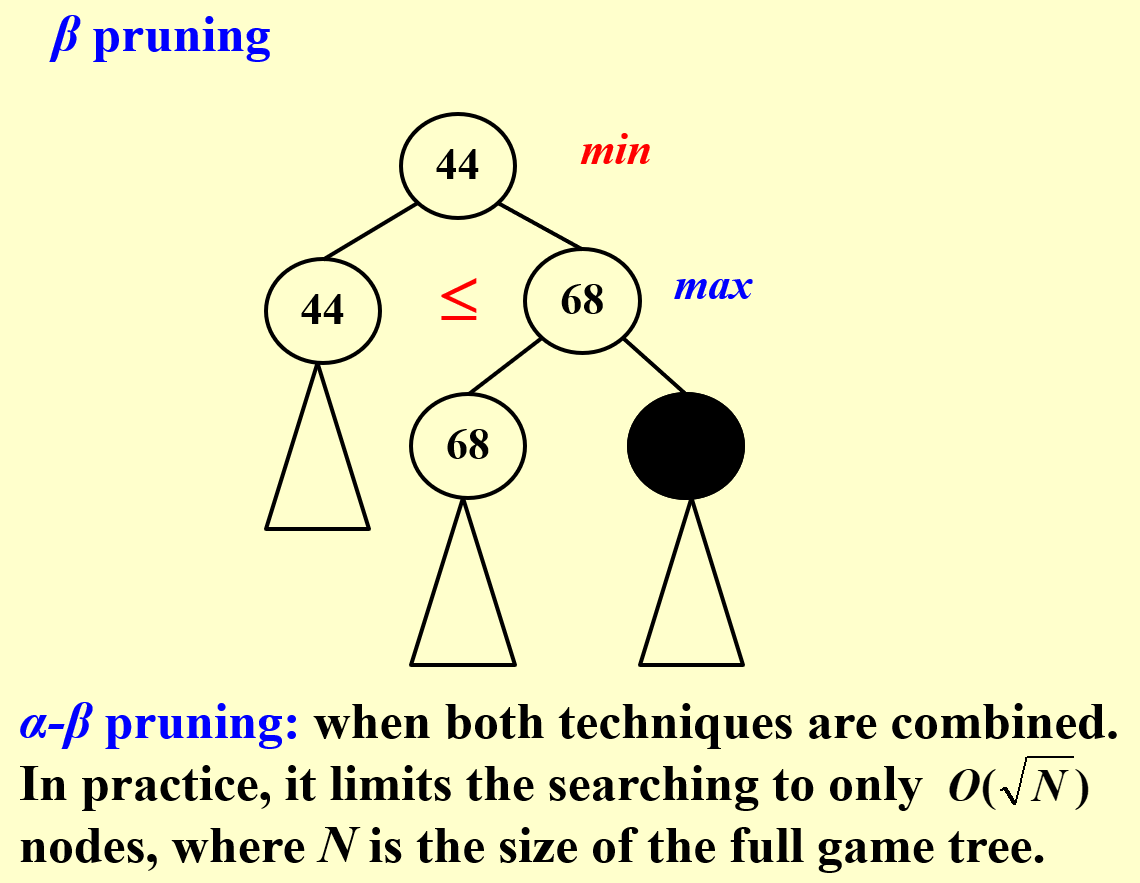
20240406172423

一目了然。

评论