Lecture 7: Divide and Conquer¶
分治法。关于 Closest Pair Problem 查阅 PPT。这里主要介绍对于分治法的递推式
\[
T(N) = aT(n/b) + f(N)
\]
的三种时间复杂度分析方法。
1 Substitution Method¶
先猜后证。
这里举两个例子。
正确的方法
例如我们有递推式
\[
T(N) = 2T(\lfloor N/2 \rfloor) + N
\]
对此进行分析。
我们猜测 \(T(N)=O(NlogN)\)。证明如下:
在假设 \(T(N)=O(NlogN)\) 的情况下,对任意的 \(m<N\) 都成立,那么这里取 \(m=\lfloor N/2 \rfloor\)。则存在常数 \(c>0\),使得 $$ T(\lfloor N/2 \rfloor) \le c \lfloor N/2 \rfloor log (\lfloor N/2 \rfloor) $$
那么根据题干的递推式,可得:
\[
\begin{aligned}
T(N)
&= 2T(\lfloor N/2 \rfloor) + N \\
&\le 2c \lfloor N/2 \rfloor log (\lfloor N/2 \rfloor) + N\\
&\le cN(logN-log2) + N\\
&\le cNlogN\\&(for\ c \ge 1)
\end{aligned}
\]
从而答案正确。
错误的示范
例如我们还是用这个递推式
\[
T(N) = 2T(\lfloor N/2 \rfloor) + N
\]
对此进行另一种猜测。
我们猜测 \(T(N)=O(N)\)。证明如下:
在假设 \(T(N)=O(N)\) 的情况下,对任意的 \(m<N\) 都成立,那么这里取 \(m=\lfloor N/2 \rfloor\)。则存在常数 \(c>0\),使得 $$ T(\lfloor N/2 \rfloor) \le c \lfloor N/2 \rfloor $$
那么根据题干的递推式,可得:
\[
\begin{aligned}
T(N)
&= 2T(\lfloor N/2 \rfloor) + N \\
&\le 2c \lfloor N/2 \rfloor+ N\\
&\le cN+ N\\
&\le (c+1)N = O(N)\\&(for\ c \ge 1)
\end{aligned}
\]
从而答案正确。吗?
错误! 在运用这种方法的时候需要证明 "Exact Form",猜测的是 \(T(N)\le cN\),证明到最后的常数就应该是 \(c\),而没有后面的 \(+N\)。
2 Recursion-tree Method¶
可以单独使用,也可以和先猜后证一起使用。
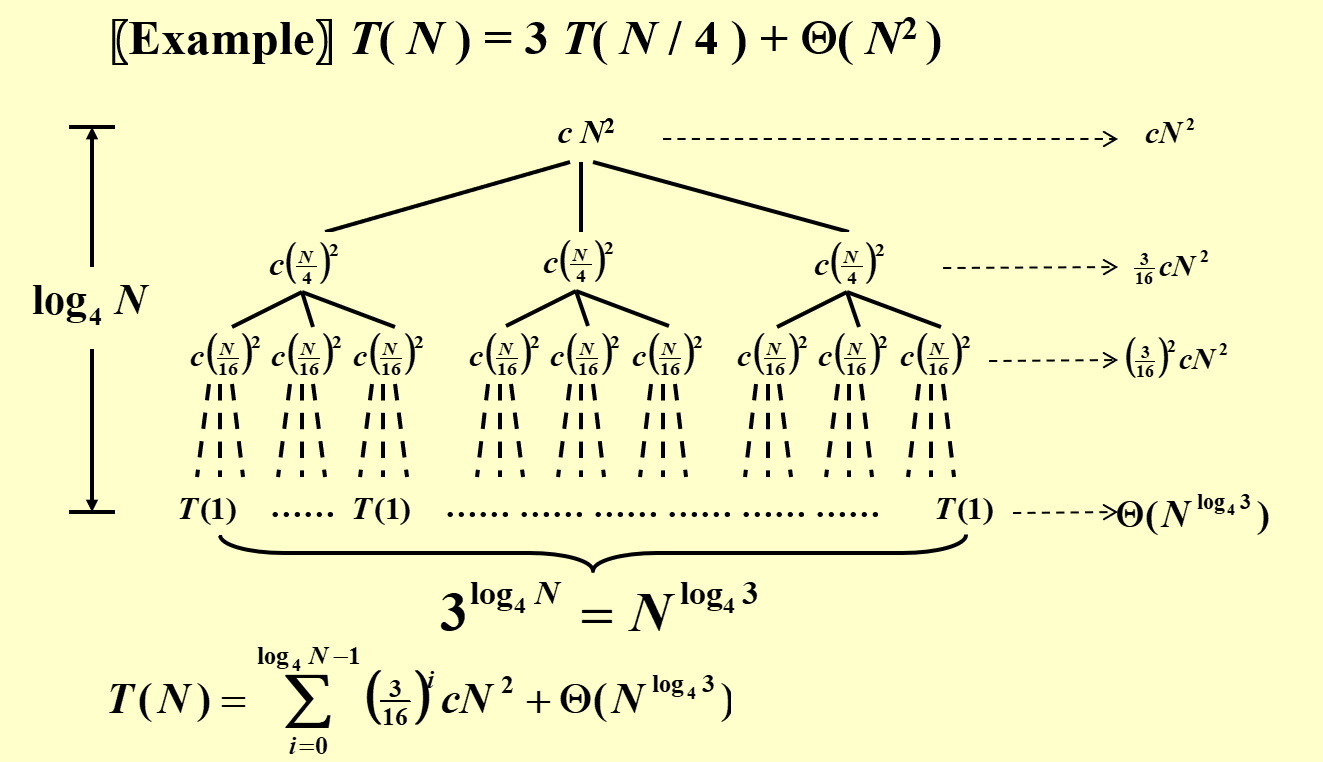
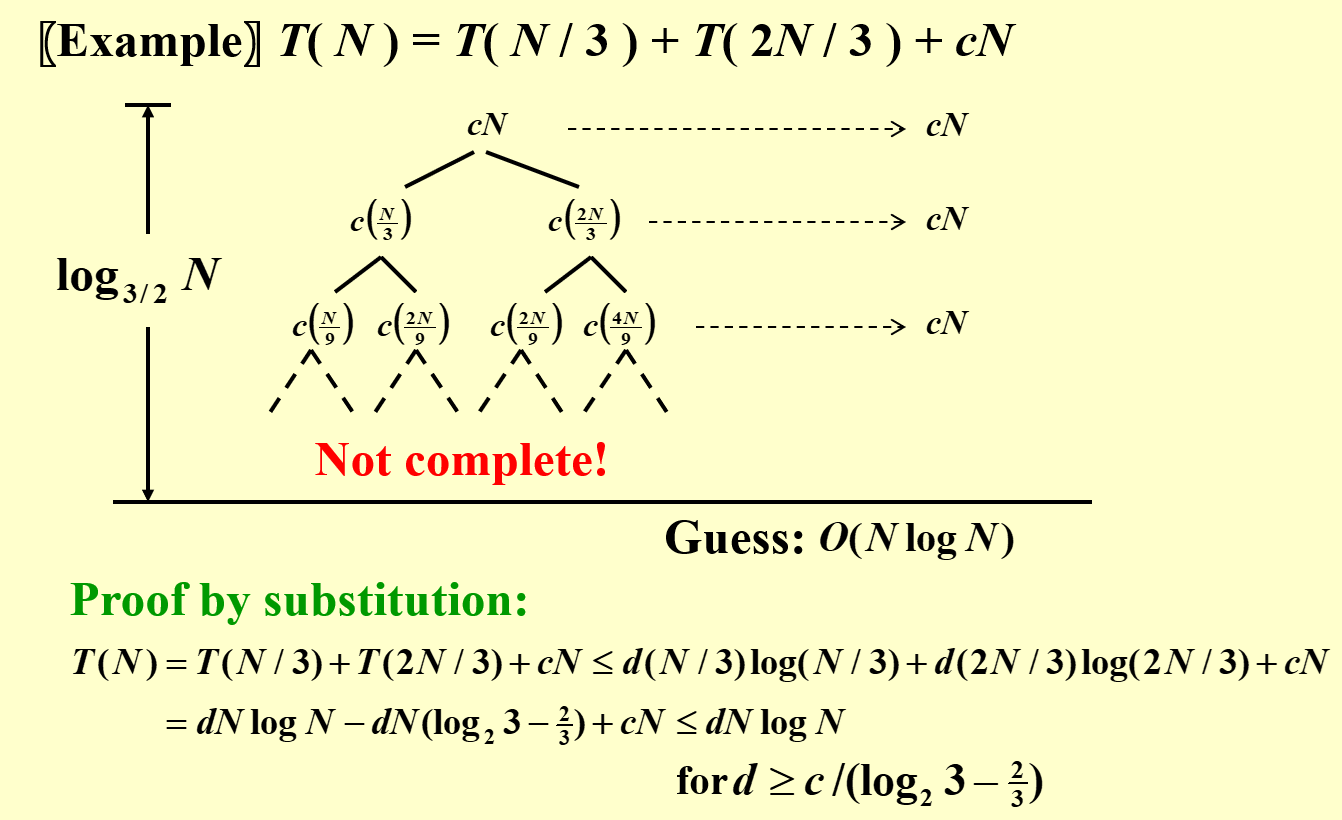
3 Master Theorem¶
少废话。直接上图



三种主定理,按照具体情况具体分析即可。注意主定理并不能涵盖所有的情况!