跳转至

Lecture 8: Dynamic Programming

动态规划。

Solve sub-problems just once and save the answers in a table.

1 Example: Fibonacci Number

使用传统的递归方法:

C
1
2
3
4
5
6
int fib(int n)
{
    if (n <= 1)
        return n;
    return fib(n - 1) + fib(n - 2);
}

对此进行性能分析：\(T(N) \ge T(N-1) + T(N-2)\)，推导出了 \(T(N) \ge F(N)\)。

问题出在，我们在递归过程中，重复计算了很多次相同的子问题。如果我们能将这些重复的子问题的解放在一张表中（或者就是简单地保存下来），那么我们就可以避免重复计算。

C
1
2
3
4
5
6
7
8
9
int fib(int n)
{
    int f[n + 1];
    f[0] = 0;
    f[1] = 1;
    for (int i = 2; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];
    return f[n];
}

显然这种算法的时间复杂度低很多，为 \(O(N)\)。

2 Example: Ordering Matrix Multiplication

要找到一种使得开销最小的乘法顺序，我们使用这种动态规划的思想。计算任意一个矩阵链的最小乘法次数，我们可以将其分解为两个子链的最小乘法次数，但是这个分解方式就有很多种，我们需要找到最优的那种。

\[ m_{ij} = \left \{ \begin{aligned} 0 & \quad i = j \\ \min_{i \le k < j} \{ m_{ik} + m_{k+1,j} + p_{i-1}p_kp_j \} & \quad i < j \end{aligned} \right. \]

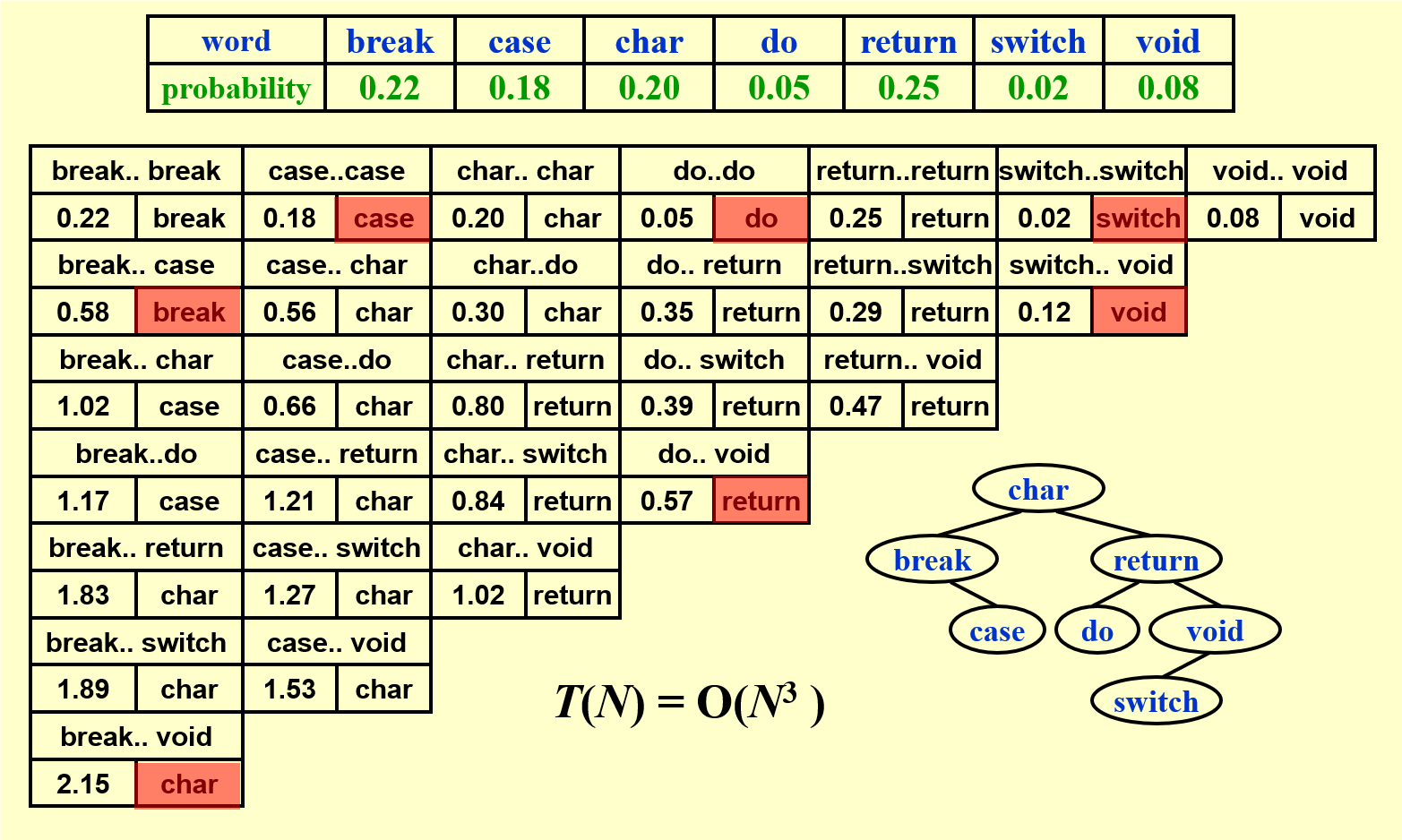
3 Example: Optimal Binary Search Tree

需要找到一种使得平均查询时间最小的树结构，也即需要使

\[ T(N) = \sum\limits_{i=1}^{N} p_i\cdot (1+d_i) \]

最小。一种很 Greedy 的想法就是把 freq 最大的放在根节点。这种虽然做出来不一定是最优解，但是却给我们以启示：我们根据“谁来当根节点”作为这种遍历的指标。

具体推导可以看 PPT，最后解决问题的方式是自底向上，从只有一个结点的树开始一步一步构造。

92235c5b4d8c4c1bf60221ce735d174b

4 Example: All-Pairs Shortest Path

Floyd 算法（动态规划）。

与前面的例子类似，我们还是维护一个动态规划的数组。

\[ D^k[i][j]=min\{length\ of\ path\ i \rightarrow \{l \le k\} \rightarrow j\} \]

这代表从 i 到 j 的，中间经过 k 个结点的最短路径。很容易知道当我们从 k 为 0 的时候开始遍历，最后 k 到 N-1 的时候一定得到的是最优解。

如何进行“状态转移”呢？当我们已经知道了 \(D^{k-1}\) 的信息之后：

  1. 如果我们不想将 k 加入最短路径，直接让 \(D^k\) 继承上一个值即可；
  2. 如果想，那么就是把 i 到 k 的最短路径和 k 到 j 的最短路径加起来就行了。

所以：

\[ D^k[i][j]=min\{ D^{k-1}[i][j],D^{k-1}[i][k]+D^{k-1}[k][j] \},\ k\ge 0 \]

给出代码：

C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
void AllPairs(A[][], D[][], int n)
{
    int i,j,k;
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
            D[i][j]=A[i][j];

    for(k=0;k<n;k++)
        for(i=0;i<n;i++)
            for(j=0;j<n;j++)
                if(D[i][k]+D[k][j]<D[i][j])
                    D[i][j]=D[i][k]+D[k][j];
}

\(T(N) = O(N)\).

5 Example: Product Assembly

第 i 个 stage 来源于上一个 stage，它可以是由别的生产线转移而来，也可以是自己这条生产线。

6 Summary

总结一下。

DP 的特征：

  • 最优子结构
  • 重叠子问题

设计 DP 方法：

  • 描述最优解的样子
  • 递归地定义最优值
  • 以某一顺序来计算
  • 最后重构解法（选）

评论