跳转至

Introduction to the Microprocessor and Computer

Outline:

  • Overview of Intel microprocessors
  • Discussion of history of computers
  • Function of the microprocessor
  • Computer data formats
  • Terms and jargon

Historical Background

  • 第一台通用的、可编程的电子计算机是 1946 年由美国宾夕法尼亚大学的约翰·普雷斯班设计的 ENIAC（Electronic Numerical Integrator and Computer）。可编程相比重新设计硬件更加灵活。
  • 冯·诺依曼（John von Neumann）在 1945 年提出了一种新的计算机结构，这种结构被称为冯·诺依曼结构。这种结构的特点是程序和数据存储在同一块存储器中，程序可以被当作数据来处理。
  • 起初的编程是用机器码实现的，由一系列的 0 和 1 组成。
  • 1950 年代 UNIVAC 等系统出现，这些系统使用汇编语言编程，汇编语言是一种符号化的机器码。
  • 1957 年 Grace Hopper 发明了第一个高级语言，称为 FLOWMATIC。同年 IBM 发明了 FORTRAN 语言。Grace Hopper 也是 COBOL 语言的发明者之一，她也发现了世界上第一个 bug（1947），是一只卡在计算机中的飞蛾。

进入微机时代：

  • 1971 年，Intel 公司推出了 4004 微处理器，这是第一款集成电路微处理器。4004 是一款 4 位的、能寻址 4096 个字节的存储器，其指令集包含 45 条指令。其速度比 ENIAC 还是慢，但是其重量小于 1 盎司。
  • 1978 年，Intel 推出了 8086 微处理器，使用了 IA-32 架构，含有 16 位的寄存器和 16 位的 data bus，内存管理使用了分段的技术。
  • 1982 年，Intel 发布 80286 微处理器，引入了 protected mode。
  • 1985 年，Intel 发布 80386 微处理器，是 IA-32 架构的第一款 32 位处理器，寄存器为 32 位，且低 16 位保持前几代的寄存器功能，维持了向后兼容性。同时其提供了虚拟 8086 模式，且支持了内存的分页，page size 为 4KB。
  • 1989 年，Intel 发布 80486 微处理器，提供了内置的浮点运算单元 x87，提供了 8KB 的一级缓存。
  • 1993 年，Intel 发布 Pentium 微处理器，引入了第二条执行流水线，实现了超标量的设计，同时引入了分支预测技术。
  • 1995-1999 年，相继发布了 Pentium Pro、Pentium II、Pentium III 微处理器。
  • 2000-2006 年，发布 Pentium 4 系列处理器。

Some Technical Terms

  • RISC：从 Pentium Pro 开始，Intel 在 CISC 指令集下实现的是 RISC 设计，即将 CISC 指令集转换为 RISC 指令集再执行，但同时能够兼容 CISC 指令集。
  • 乱序执行：超标量设计带来了 ILP（Instruction Level Parallelism），但是由于数据相关性，指令之间的执行顺序可能会受到影响，因此需要乱序执行技术来解决这个问题。
乱序执行的例子
Text Only
1
2
3
4
5
6
r1 = r4 / r7    # Assmue divide takes 20 cycles
r8 = r1 + r2
r5 = r5 + 1
r6 = r6 - r3
r4 = r5 + r6
r7 = r8 * r4

假设这里的 look ahead window = 4，运用三条流水线。如果是顺序执行，因为数据依赖关系，其执行情况如下图：

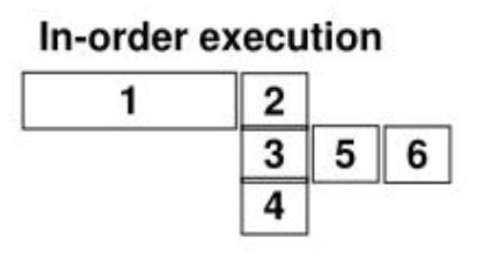
如果使用乱序执行，维护一个数据流图：

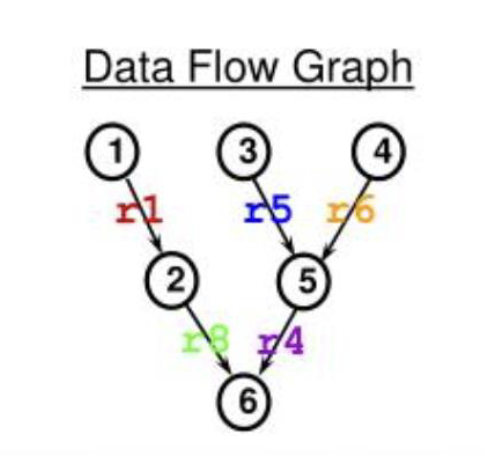
按照数据流图可以来优化执行顺序：

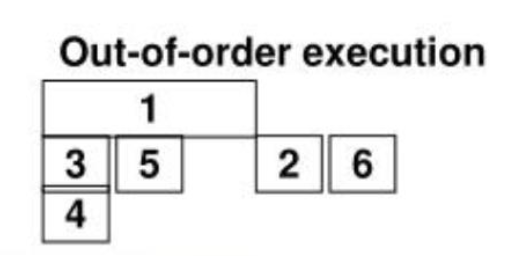
  • SIMD：单指令多数据流，即一条指令可以同时处理多个数据，例如 MMX、SSE、AVX 等。
  • Hyper-Threading：一种多线程技术，可以让一个物理核心模拟出多个逻辑核心，提高了 CPU 的利用率。
Intel 64 Architecture

软件寻址 64 位，物理地址寻址最多 52 位。这种技术也被称为 IA-32e 模式，包含 64-bit 模式和兼容模式。

Number Systems

这一部分比较基础，略过。

Computer Data Formats

包含 ACSCII、Unicode、BCD、有符号和无符号整数、浮点数等等。

  • ACSCII：American Standard Code for Information Interchange，标准的 ASCII 是一种 7 位的编码方式，包含 128 个字符。
    • 其中，第 8 位（MSB）用来做校验位。在打印机中，这一位的 0 代表 alphanumeric，1 代表 graphics。
    • Extended ASCII：使用 8 位来表示字符（最高位为 1），包含 256 个字符，存储了一些外国字符、注音、希腊字母、制表符等。
  • Unicode：大多数基于 Windows 的应用使用 Unicode，每个字符使用 16 位来表示。
    • 0000H-00FFH 和标准 ASCII 一样，00FFH-FFFFH 用来表示其他字符。
  • BCD：Binary Coded Decimal，用 4 位二进制数来表示一个十进制数，包含 0-9 的数字。
Packed & Unpacked BCD
  • Packed BCD：两个 BCD 数字存储在一个字节中，每个数字占 4 位，用于微处理器中的 BCD 加法减法。
  • Unpacked BCD：每个 BCD 数字占 1 字节，即 8 位，一般是键盘输入的数据。

例如，12 的 Packed BCD 表示为 0001 0010，Unpacked BCD 表示为 0000 0001 0000 0010。

复杂的计算情况下一般不用 BCD 码。

  • Byte-sized Data：字节大小的数据，一般用来存储字符、整数等。
  • Word-sized Data：字大小（16 位）的数据，一般用来存储地址、整数等。在 x86 架构中，数据以小端序存储。
大小端问题

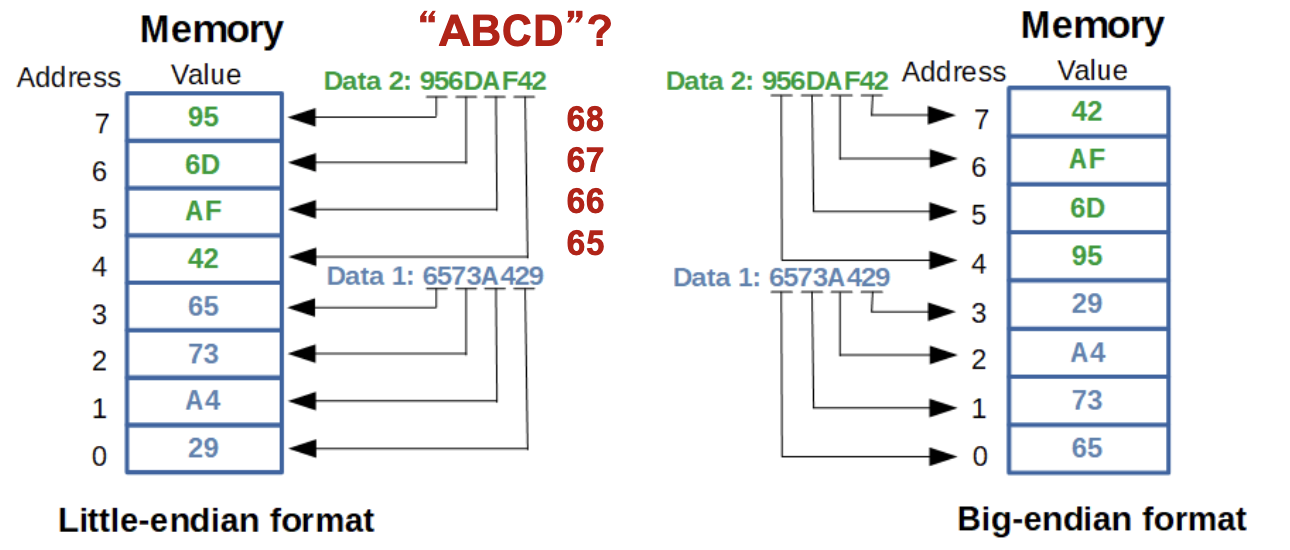
需要注意的是，x86 中数据是小端存储，但是字符串、指令等是大端存储。

  • Double Word-sized Data：双字大小（32 位）的数据，也就是所谓的 DWORD。
  • Real Numbers：实数，也就是浮点数。IEEE 754 标准定义了浮点数的表示方法。

这里需要注意一些别名符号，MASM 是一个 x86 汇编器，其定义了一些别名符号：

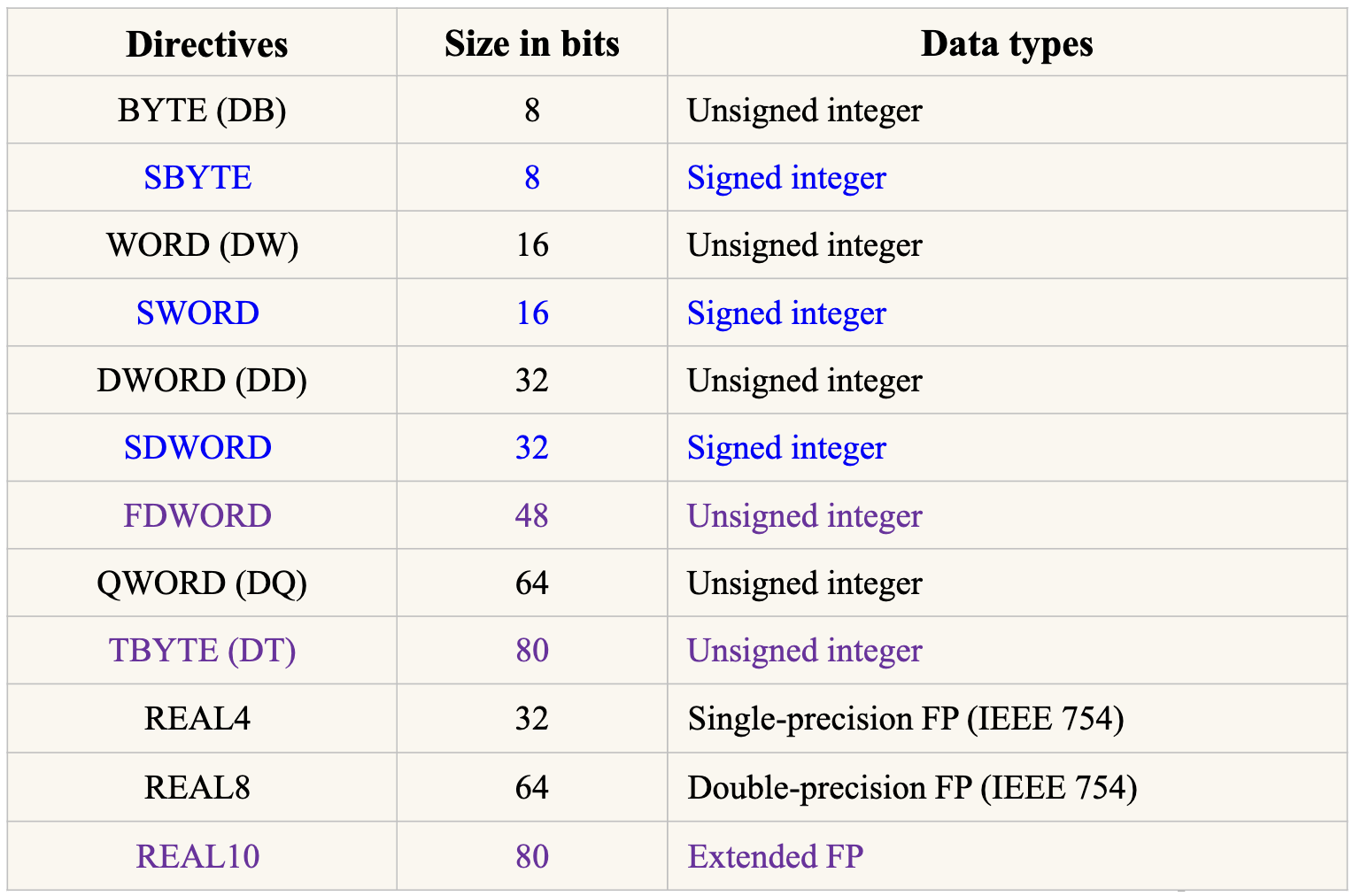
The IEEE 754 Format

由 William Morton Kahan 等人于 1985 年提出，定义了浮点数的表示方法。Kahan 也获得了 1989 年的 ACM 图灵奖，被誉为“浮点数之父”。

Format

该标准将浮点数表示为：

\[ (-1)^{\text{sign bit}} \times (1+\text{fraction}) \times 2^{\text{exponent-bias}} \]

对于单精度浮点数，其格式为：

Text Only
1
| Sign (1 bit) | Exponent (8 bits) | Fraction (23 bits) |

对于双精度浮点数，其格式为：

Text Only
1
| Sign (1 bit) | Exponent (11 bits) | Fraction (52 bits) |

Why not 2's Complement?

  • 没有无符号浮点数，用 2's Complement 没有任何的额外好处。
  • 补码的负数比正数多一个，导致不对称。
  • 科学计算的时候实际上是区分 +0 和 -0 的，而 2's Complement 无法区分。
  • 等等等等。

Special Values

Exponent 部分为全 0 或全 1 时，表示特殊值：

  • 0：Exponent 全 0，Fraction 全 0，表示 +0 或 -0，看 Sign 位。
  • 无穷大：Exponent 全 1，Fraction 全 0，看 Sign 位决定正负。
  • NaN：Exponent 全 1，Fraction 非 0，表示 Not a Number。

Subnormal Numbers

  • Normal Numbers：Exponent 不全 0 也不全 1。
  • Subnormal Numbers：Exponent 全 0，Fraction 非 0。这个数很小，小到超过了 IEEE 754 的精度范围，因此需要特殊处理。这个时候的数字表示有一些差异：
\[ (-1)^{\text{sign bit}} \times (0+\text{fraction}) \times 2^{1-\text{exponent-bias}} \]
  • Subnormal Numbers 可能会引发性能的剧烈下降。

Rounding

  • TiesToEven：靠近偶数的时候向偶数靠拢。（默认）
  • TiesAwayfromZero
  • TiesToZero
  • TiesTowards +∞
  • TiesTowards -∞

Addition

对阶、相加、舍入。

对阶操作的存在会导致大数吃小数的问题，因此需要进行舍入操作。

一些公式可以进行重写，会有性能和精度的变化。例如 Herbie 等工具可以自动优化这些公式。

重写浮点表达式的例子
\[ \sqrt{x+1} - \sqrt{x} = \frac{1}{\sqrt{x+1} + \sqrt{x}} \]

精度从 70.6% 提升到 99.5%，性能从 1.0x 下降到 0.7x。

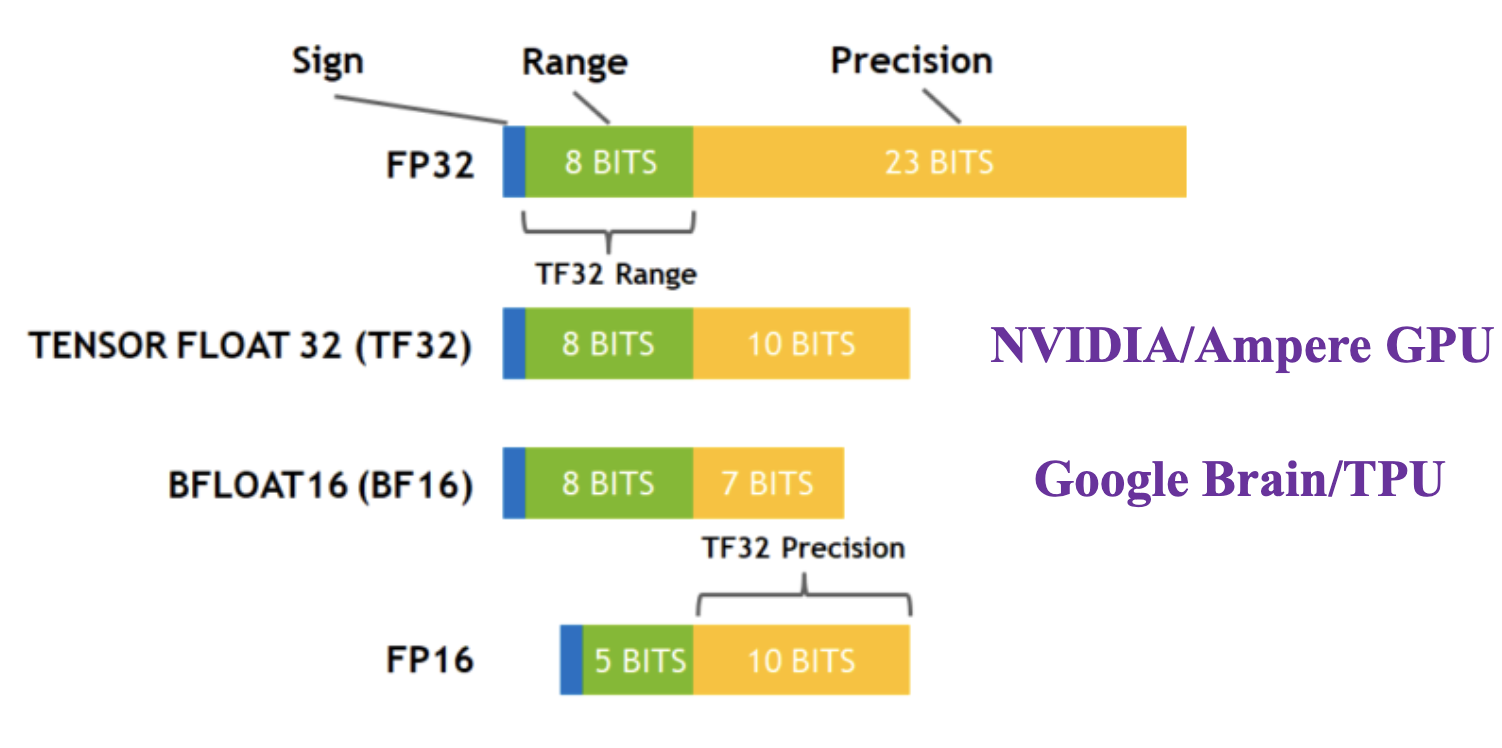
New Floating-point Format for AI

为了便于 AI 计算，一些新的浮点数格式被提出，例如 Bfloat16、TF32、FP16 等。

评论