Chap3. Trees

本章介绍一种”一对多“的数据结构：树。其中重点介绍二叉树，包含其表达方式、遍历访问、以及树衍生出的特殊结构，包括二叉搜索树、最小最大堆、并查集等。

3.1 Preliminaries

基本知识在离散数学中已有涉及。

注意：

• 树可以是空的
• \(N\)结点树有\(N-1\)条边
• 树结点的degree的定义不同于图。树的结点的degree是子树的数量
• 树的degree为所有结点degree的最大值
• 结点的depth为root到该节点的深度；结点的height为该节点到leaf的最长长度。具体的计数情况看题目要求

3.2 Implementation

• List Representation:

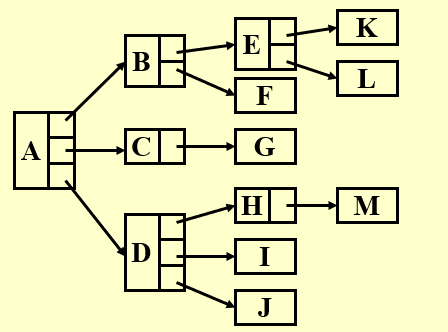
缺点是需要根据具体情况来确定每一个node的大小。

• FirstChild-NextSibling Representation:

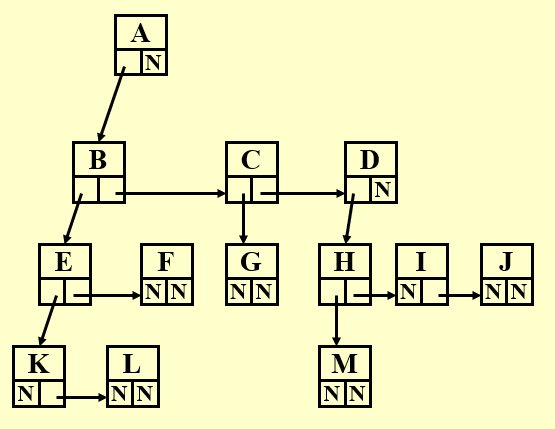
每个结点有两个指针域，分别为大儿子和下一个兄弟。这种方式能把任何树结构化为二叉树，且对于同一棵树能有不同的表示方式（children的顺序可以改变）。

3.3 Binary Trees

A binary tree is a tree in which no node can have more than two children.

可以作为表达式树（Expression trees/Syntax trees）。

二叉树的左儿子和右儿子是不一样的！

性质：

• The maximum number of nodes on level \(i\) is \(2^{i-1},\ i\ge1\).
• The maximum number of nodes in a binary tree of depth \(k\) is \(2^{k}-1,\ k\ge1\).
• For any nonempty binary tree, \(n_{0}=n_{2}+1\) where \(n_{i}\) is the number of leaf nodes of degree \(i\).

3.3.1 Tree Traversals

1. Preorder

void preorder(tree_ptr tree)
{
    if(tree){
        visit(tree);
        for(each child C of tree)
            preorder(C);
    }
}
void preorder_binary(tree_ptr tree)// for binary trees
{
    if(tree){
        visit(tree);
        preorder_binary(tree->leftchild);
        preorder_binary(tree->rightchild);
    }
}

2. Inorder (For binary trees)

void inorder_binary(tree_ptr tree)// for binary trees
{
    if(tree){
        inorder_binary(tree->leftchild);
        visit(tree);
        inorder_binary(tree->rightchild);
    }
}
void iter_inorder(tree_ptr tree)// iterative
{
    Stack S=CreateStack();
    while(True)
    {
        for(;tree;tree=tree->leftchild)
            Push(tree,S);
        tree=Top(S);
        Pop(S);
        if(!tree) break;
        visit(tree);
        tree=tree->Right;
    }
}

3. Postorder

void postorder(tree_ptr tree)
{
    if(tree){
        for(each child C of tree)
            postorder(C);
        visit(tree);
    }
}
void postorder_binary(tree_ptr tree)// for binary trees
{
    if(tree){
        postorder_binary(tree->leftchild);
        visit(tree);
        postorder_binary(tree->rightchild);
    }
}

4. Levelorder

void levelorder(tree_ptr tree)
{
    enqueue(tree);
    while(queue is not empty)
    {
        visit(T=dequeue());
        for(each child C of T)
            enqueue(T);
    }
}

相当于每一层的结点都入队，遍历时选取结点出队即可。

3.3.2 Threaded Binary Trees

Rules:

1. If Tree->Left is NULL, replace it with a pointer to the inorder predecessor of Tree.
2. If Tree->Right is NULL, replace it with a pointer to the inorder sucessor of Tree.
3. There must not be any loose threads. Therefore a threaded binary tree must have a head node of which the left child points to the first node.

把空的Leaf结点利用起来，用以指向中序遍历的前后结点。

在存储的时候需要设定一个flag用以标志是线索还是真正的孩子。

typedef  struct  ThreadedTreeNode  *PtrTo  ThreadedNode;
typedef  struct  PtrToThreadedNode  ThreadedTree;
typedef  struct  ThreadedTreeNode {
       int                  LeftThread;   /* if it is TRUE, then Left */
       ThreadedTree     Left;      /* is a thread, not a child ptr.   */
       ElementType  Element;
       int                  RightThread; /* if it is TRUE, then Right */
       ThreadedTree     Right;    /* is a thread, not a child ptr.   */
}

3.4 The Search Tree ADT (Binary Search Trees)

3.4.1 ADT

A binary search tree is a binary tree. It may be empty.

If it is not empty, it satisfies the following properties:

1. Every node has a key which is an integer, and the keys are distinct.
2. The keys in a nonempty left subtree must be smaller than the key in the root of the subtree.
3. The keys in a nonempty right subtree must be larger than the key in the root of the subtree.
4. The left and right subtrees are also binary search trees.

• Objects: A finite ordered list with zero or more elements.
• Important Operations:
• Find
• FindMin/FindMax
• Insert
• Delete

3.4.2 Implementations

1. Find:

Position Find(ElementType X, SearchTree T)
{
    if(T==NULL) return NULL;
    if(X<T->Element) return Find(X, T->Left);
    else if(X>T->Element) return Find(X, T->Right);
    else return T;
}

\(T(N)=S(N)=O(d)\), where \(d\) is the depth of X.

2. FindMin/FindMax:

Position FindMin(SearchTree T)// recursive version
{
    if(T=NULL) return NULL;
    else if(T->Left==NULL) return T;
    else return FindMin(T->Left);
}
Position FindMax(SearchTree T)// iterative version
{
    if(T!=NULL)
        while(T->Right!=NULL)
            T=T->right;
    return T;
}

\(T(N)=O(d)\).

3. Insert:

根本思想：从根节点开始一层一层比对，直到找到空位或者已经存在待插入元素结束。

SearchTree Insert( ElementType X, SearchTree T ) 
{ 
    if ( T == NULL ) 
    { /* Create and return a one-node tree */ 
     T = malloc( sizeof( struct TreeNode ) ); 
     if ( T == NULL ) FatalError( "Out of space!!!" ); 
     else 
        { 
         T->Element = X; 
         T->Left = T->Right = NULL; 
        } 
    }
    else  /* If there is a tree */
         if ( X < T->Element ) T->Left = Insert( X, T->Left ); 
 else if ( X > T->Element ) T->Right = Insert( X, T->Right ); 
    /* Else X is in the tree already; we'll do nothing */ 
    return  T;
}

\(T(N)=O(d)\).

4. Delete:

分为几种情况：

• 删除叶节点：直接设置为NULL即可
• 删除1度结点：儿子跟上来
• 删除2度结点：左子树最大值或右子树最小值替代之

SearchTree Delete(ElementType X, SearchTree T)
{
    if(T==NULL) Error("NOT FOUND");
    else
    {
        if(X<T->Element) T->Left=Delete(X, T->Left);
        else if(X>T->Element) T->Right=Delete(X, T->Right);
        else if(T->Left&&T->Right)
        {
            Position temp=FindMin(T->Right);
            T->Element=temp->Element;
            T->Right=Delete(T->Element, T->Right);  
        }
        else
        {
            Position temp=T;
            if(T->Left==NULL) T=T->Right;
            else if(T->Right==NULL) T=T->Left;
            free(temp);
        }
    }
    return T;
}

\(T(N)=O(h)\), where \(h\) is the height of tree.

注意：如果删除次数不多，可以用lazy deletion方案，即将需要删除的结点仅作标记而不是真的删除，遍历时自动跳过这些结点即可。

3.4.3 Average-Case Analysis

Q: Place \(n\) elements in a binary search tree. How high can this tree be?

A: Depends on the order of insertion. From \(log\ n\) to \(n\).

3.5 Priority Queues (Heaps)

3.5.1 ADT

• Objects: A finite ordered list with zero or more elements.
• Important Operations:
• Insert
• DeleteMin/DeleteMax

3.5.2 Implementations

实际上使用数组来实现。（完全二叉树）

Defination: A binary tree with n nodes and height h is complete iff its nodes correspond to the nodes numbered from 1 to n in the perfect binary tree of height h.

每一层先占据从左到右的结点。只有最后一层是有可能不满的。

A complete binary tree of height \(h\) has between \(2^{h}\) and \(2^{h+1}-1\) nodes. Thus, \(h=\lfloor log\ N \rfloor\).

Array Representation: BT[n+1] (BT[0] is not used).

对于数组形式存储的完全二叉树，对于下标为\(i\)的结点（\(1\le i \le n\)），其父亲节点下标（如果有的话）为\(\lfloor i/2 \rfloor\)，左儿子节点下标（如果有的话）为\(2i\)，其右儿子节点下标（如果有的话）为\(2i+1\)。

完全二叉树能够用来实现最小堆/最大堆。

A min tree is a tree in which the key value in each node is no larger than the key values in its children (if any). A min heap is a complete binary tree that is also a min tree.

Basic operations:

1. Insert:

void Insert(ElementType X, MinHeap H)
{
    int i;
    if(IsFull(H))
        Error("FULL");

    for(i=++H->Size;H->Elements[i/2]>X;i/=2)// H->Element[0] is the sentinel, no larger than the minimum in the heap!
        H->Elements[i]=H->Elements[i/2];// percolate UP
    H->Elements[i]=X;
}

\(T(N)=O(logN)\).

2. DeleteMin: 重点！

ElementType DeleteMin(MinHeap H)
{
    if(IsEmpty(H)) Error("EMPTY");
    int parent, child;
    ElementType MinElement, LastElement;
    MinElement=H->Elements[1];
    LastElement=H->Elements[H->Size--];

    for(parent=1;parent*2<=H->Size;parent=child)// percolate DOWN
    {
        child=parent*2;
        if(child!=H->Size && H->Elements[child+1]<H->Elements[child])// choose if the right child or not
            child++;
        if(LastElement>H->Elements[child])// doesn't obey the rule
            H->Elements[parent]=H->Elements[child];
        else break;// is the right position now
    }
    H->Elements[parent]=LastElement;
    return MinElement;
}

3. BuildHeap:

• 采用逐个插入的方式建堆，\(T(N)=O(NlogN)\)
• 采用先直接放置再进行调整方法建堆：从倒数第一个有孩子的结点Heap[n/2]开始，将其子树进行调整（看作插入操作），逐步调整至Heap[0]，自然建成堆。\(T(N)=O(N)\)

应用：给\(N\)个元素找第\(k\)大的元素。可以采用线性时间建堆并调用\(k\)次DeleteMin即可。

3.5.3 d-Heaps

All nodes have \(d\) children.

3.6 The Disjoint Set ADT

并查集，实现等价类问题。

3.6.1 ADT

• Objects: Sets and their elements
• Important Operations:
• Union
• Find

3.6.2 Implementations

1. Union:

思路：将一个集合根节点作为另一个集合子树结点

Union by size/by height: 避免树高度过长问题。需要将S[root]设置为-size或者是-height.

void Union_bySize(Set S, int root1, int root2)// S[root]=-number of elements
{
    if(S[root2]<S[root1])
    {
        S[root2]+=S[root1];
        S[root1]=root2;
    }else
    {
        S[root1]+=S[root2];
        S[root2]=root1;
    }
}
void Union_byHeight(Set S, int root1, int root2)// S[root]=-height
{
    if(S[root2]<S[root1]) S[root1]=root2;
    else{
        if(S[root1]==S[root2]) S[root1]--;// height+1
        S[root2]=root1;
    }
}

\(N\) union and \(M\) find operations is now \(T=O(N+Mlog_{2}N)\).

2. Find:

找到对应的树根即可。

路径压缩：减小树的高度。找根的过程中每一个中间节点最后都直接连接于根节点。

Set Find_re(ElementType X, Set S)// recursive
{
    if(S[X]<=0) return X;
    else return S[X]=Find_re(S[X], S);
}
Set Find_it(ElementType X, Set S)// iterative
{
    ElementType root, trail, lead;
    for(root=X;S[root]>0;root=S[root]) ;
    for(trail=X;trail!=root;trail=lead)
    {
        lead-S[trail];
        S[trail]=root;
    }
    return root;
}

评论