Chap4. Graph Algorithms¶

本章介绍一种”多对多“的数据结构：图。包含其定义和一些性质，以及其上存在的一些算法：拓扑排序、最短路径、网络流、最小生成树问题等。

4.1 Definitions¶

主要部分在离散数学中已经涉及过。

注意，在这里：

禁止自环（self loop）
不考虑多图（两个结点之间超过1条边）
可以不连通
degree代表和该结点有关的边数
Given G with \(n\) vertices and \(e\) edges, then \(e=(\sum\limits_{i=0}^{n-1} d_{i})/2\), where \(d_{i}=\mathrm{degree}(v_{i})\).

4.2 Implementations¶

存储方式主要两种：邻接矩阵和邻接表。

4.2.1 Adjacency Matrix¶

For a graph with \(n\) vertices, use adi_mat[n][n] to store the relations between vertices.

adj_mat[i][j]=1 if \((v_{i},v_{j}) \in E(G)\), and 0 otherwise.

如果G是无向图，则该矩阵为对称，这样就可以使用一维数组对半存储：\(a_{ij}\) 的索引是i*(i+1)/2+j（下标从0开始）。

4.2.2 Adjacency Lists¶

\(N\) 个链表，每个链表将其连接的点（如果是有向图为出点）串起来。

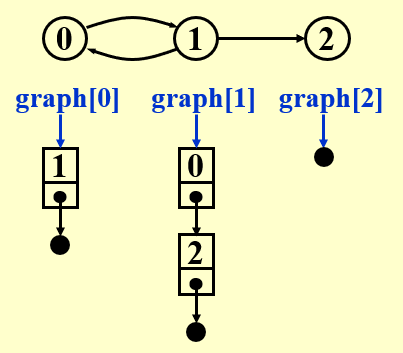
并且对于有向图，需要找到每个点的入度。有以下解决方案：

加入逆邻接表：

Multilists: 便于标记边。

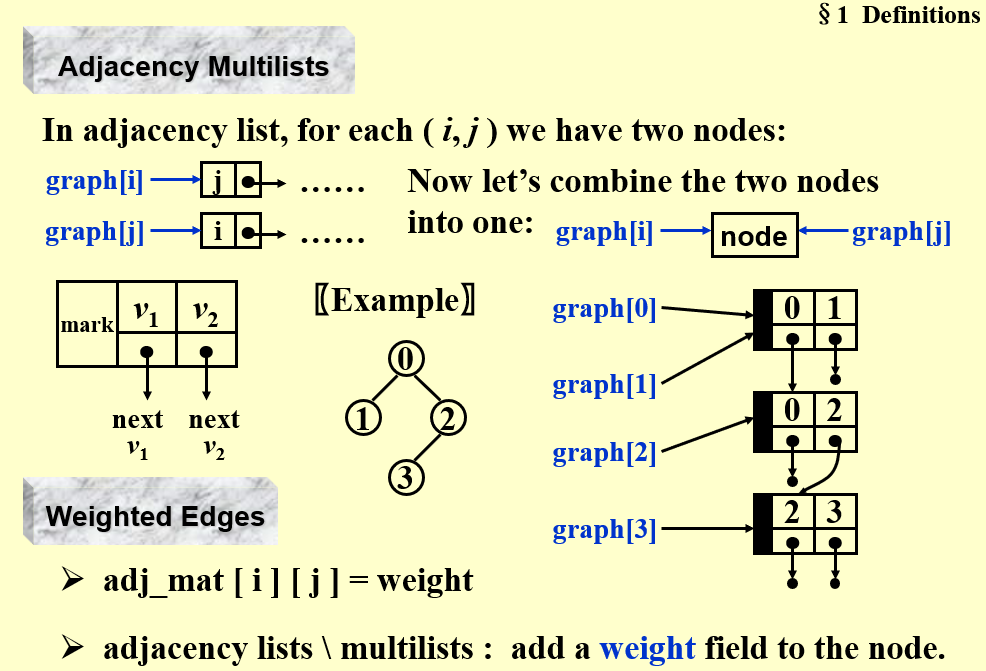
4.3 Topological Sort¶

AOV Network: Action On Vertices.

核心是图中存在a->b的关系是，得到的拓扑序列一定满足a在b之前。

Partial order: a precedence relation which is both transitive ( i->k, k->j THUS i->j ) and irreflexive ( i->i is impossible ).

A topological order is a linear ordering of the vertices of a graph such that, for any two vertices, i, j, if i is a predecessor of j in the network then i precedes j in the linear ordering.

使用队列实现算法。

C
void Topsort(Graph G)
{
    Queue Q;
    int cnt=0;
    Vertex V, W;
    for(each vertex V)
    {
        if(indegree[V]==0) enqueue(V,Q);
        while(!IsEmpty(Q))
        {
            V=dequeue(Q);
            TopNum[V]=++cnt;
            for(each W adjacent to V)
                if(--indegree[W]==0) enqueue(W,Q);
        }
    }
    if(cnt!=NumberOfVertex) Error("GRAPH HAS A CYCLE");
    free(Q);
}

4.4 Shortest Path Algorithms¶

4.4.1 Single-Source Shortest-Path Problem¶

分为有负边和无负边情况。

无负边：

Unweighted Shortest Paths: Breadth-first search

C
void Unweighted(Table T)
{
    Queue Q;
    Vertex V,W;
    enqueue(S,Q);
    while(!IsEmpty(Q))
    {
        V=dequeue(Q);
        T[V].Known=True;
        for(each W adjacent to V)
        {
            if(T[W].Dist==Inf)
            {
                T[W].Dist=T[V].Dist+1;
                T[W].Path=V;
                enqueue(W,Q);
            }
        }
    }
    free(Q);
}

需要一个Path数组来保存某个节点的前驱节点。

Weighted Shortest Paths: Dijkstra's Algorithm

基本思想是建立一个集合用以保存已经找到最短路径的结点，用这些结点来”刷新“未找到最短路径的结点。

不适用于负边！

C
void Dijkstra(Table T)
{
    Vertex V,W;
    while(True)
    {
        V=smallest unknown distance vertex;
        if(V is not found) break;

        T[V].Known=True;
        for(each W adjacent to V)
        {
            if(!T[W].Known)
            {
                if(T[V].Dist+<V,W><T[W].Dist)
                {
                    T[W].Dist=T[V].Dist+<V,W>;
                    T[W].Path=V;
                }
            }
        }
    }
}

Implementations:

V=smallest unknown distance vertex--simply scan the table--\(O(|V|)\)

\(T=O(|V|^{2}+|E|)\)
V=smallest unknown distance vertex--keep distances in a heap and call DeleteMin--\(O(log|V|)\)

Decrease T[W].Dist to T[V].Dist+<V,W>:
- Method 1: DecreaseKey--\(O(log|V|)\), \(T=O(|E|log|V|)\)
- Method 2: Insert W with updated Dist into the heap--\(T=O(|E|log|V|)\) but requires \(|E|\) space.

有负边：

C
void weighted_negative(Table T)
{
    Queue Q;
    Vertex V,W;
    enquque(S,Q);
    while(!IsEmpty(Q))
    {
        V=dequeue(Q);
        for(each W adjacent to V)
        {
            if(T[V].Dist+<V,W><T[W].Dist)
            {
                T[W].Dist=T[V].Dist+<V,W>;
                T[W].Path=V;
                if(W is not already in Q)
                    enqueue(W,Q);
            }
        }
    }
    free(Q);
}

特别地，如果图是无环图，可以以拓扑序来选择结点。

4.4.2 All-Pairs Shortest Path Problem¶

4.5 Network Flow Problems¶

每一条边代表最大容量capacity。需要有一个回溯图residual G，其边的权重代表管道的空闲量。

一种贪心算法：

Step 1: Find any path s->t;
Step 2: Take the minimun edge on this path;
Step 3: Update residual graph and remove the 0 floa edges;
Step 4: If there is still a path s->t, goto Step 1. Else, end.

这种算法与其选取路径的顺序有关，有可能得不到最优解。

解决方法：引入undo机制。找到每条边之后在residual graph中加一条反向边，权重为刚才减掉的权重。

此时\(T=O(f\cdot|E|)\)，其中\(f\)是最大流大小。

改进：不随便选择路径而是按照unweighted shortest path选择一条路径。此时\(T=O(|E|^{2}\cdot|V|)\)

4.6 Minimun Spanning Tree¶

A spanning tree of a graph G is a tree which consists of V( G ) and a subset of E( G ).

注意：

最小生成树边数为\(|V|-1\)
最小生成树存在iff图是连通的
生成树中任意加一条边，就能得到一个环

两个算法：

Prim's Algorithm:

基本思想：种树。

从任意节点开始不断挑选已经在生成树中的结点和不在生成树中的结点之间的最短边，将对应的结点加入生成树。

类似于Dijkstra算法。

\(T=O(|V|)\).

Kruskal's Algorithm:

基本思想：维持一个森林。

每个结点都是一棵树，初始一共有\(V\)棵树。不断地加边，导致树的数量减小，直至只剩下一棵树。

把边按照权重顺序排列。每次选权重最小的边，判断加入这条边会不会形成环路（等价于这条边是否连接着两个不同的树，也等价于两个结点之间本来没有通路），如果不会形成环路则加入，否则舍弃，直到只剩下一棵树即可。

C
void Kruskal(Graph G)
{   T = { } ;
    while  ( T contains less than |V|-1 edges && E is not empty ) 
    {
        choose a least cost edge (v, w) from E ;// DeleteMin
        delete (v, w) from E ;
        if  ( (v, w) does not create a cycle in T )     
         add (v, w) to T ; /*Union/Find*/
        else     
         discard (v, w) ;
    }
    if  ( T contains fewer than |V|-1 edges )
        Error ( “No spanning tree” ) ;
}

4.7 Applications of DFS¶

DFS算法：

C
void DFS(Vertex V)
{
    visited[V]=True;
    for(each W adjacent to V)
    {
        if(!visited[W])
            DFS(W);
    }
}

4.7.1 Components¶

4.7.2 Biconnectivity¶

几个定义：

Articulation Point: 关键点。把这个点以及与其相关的边删掉，图至少多一个连通分量。
Biconnected Graph: 双连通图。没有关键点的图。
Biconnected Component: 最大双连通子图。

寻找联通无向图G的双连通部分算法：

DFS构建G的生成树
找到G的关键点

4.7.3 Euler Circuits¶