跳转至

Chap6. Hashing

本章节介绍基本的散列表概念以及Hash值算法。

6.1 General Idea

核心思想是找到一个映射\(f(x)\)，其中\(x\)是所需要分类的元素，将其映射到简单而又容易计算的Hash值中。

将{}构成的集合称为散列表（Symbol Table）。

ADT:

  • Objects: A set of name-attribute pairs, where the names are unique
  • Important Operations:
  • Find
  • Insert
  • Delete

Hash Tables:

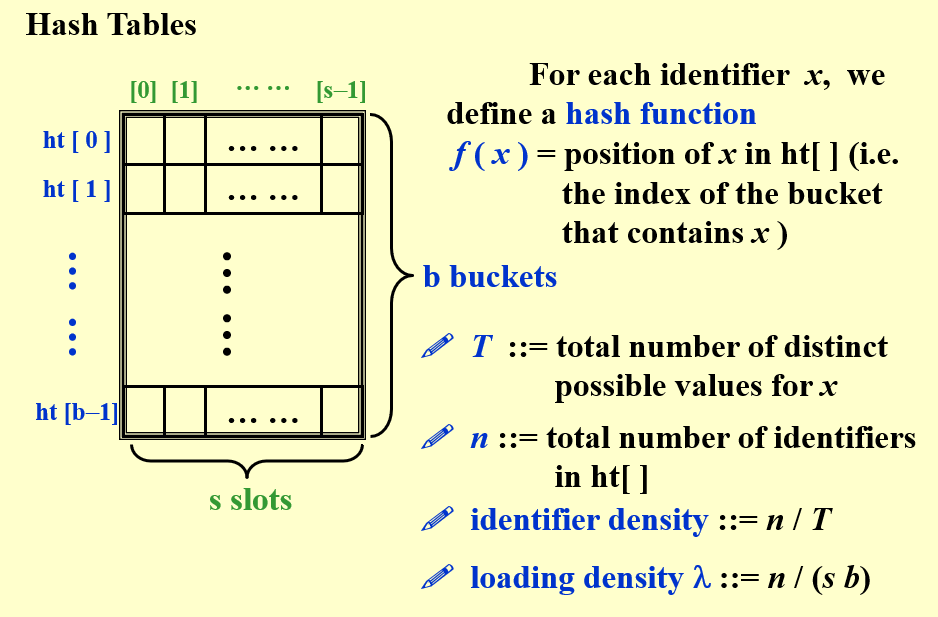
image-20240116160329937

注意上图中identifier density和loading density的定义！

两个重要概念：

  1. Collision：\(i_{1}\neq i_{2}\)，但是\(f(i_{1})=f(i_{2})\)。设计hash函数的时候需要尽量避免这种情况
  2. Overflow：某个bucket已经满了，来了一个新元素。

当\(s=1\)的时候，collision与overflow同时发生。

没有Overflow的情况下：\(T_{\mathrm{search}}=T_{\mathrm{insert}}=T_{\mathrm{delete}}=O(1)\)

6.2 Hash Function

映射函数的几个性质：

  1. 便于计算、最大程度规避collision问题
  2. 不能有偏重，即\(\forall x,\ \forall i\)，都有\(\mathrm{Probability}(f(x)=i)=1/b\)。这被称作uniform hash function。

例如取\(f(x)=x\% \mathrm{Tablesize}\)，Tablesize最好取质数。

6.3 Separate Chaining

冲突的一种解决方式。每个hash值设置成一个链表，这样就不会有collision的问题了。

但是这样的话查找不是\(O(1)\)时间，hash的优势无法体现了。

6.4 Open Addressing

冲突的另一种解决方式。选择其他的空位填补。

  1. Linear Probing:

遇到冲突就+1位，还冲突就+2位......以此类推。溢出了循环回来，取tablesize的余数。

缺点是容易造成聚堆问题。

  1. Quadratic Probing:

遇到冲突+1^2位，还冲突-1^2位，还冲突+2^2=4位，再冲突-2^2=-4位......以此类推。溢出了同样循环回来。

缺点是可能造成有空位但总是填不满的情况。但是当tablesize满足\(4k+3\)的质数形式的时候可以填满。

  1. Double Hashing:

\(f(x)=i*\mathrm{hash}_{2}(x)\)，hash_2代表另一个hash函数，要求不恒等于0.

一般采用\(\mathrm{hash}_{2}(x)=R-(x\% R)\)，其中\(R\)是一个小于TableSize的质数。

6.5 Rehashing

Q: When to rehash?

A:

  1. As soon as the table is half full
  2. When an insertion fails
  3. When the table reaches a certain load factor

评论